JEE MAIN - Physics (2005 - No. 32)
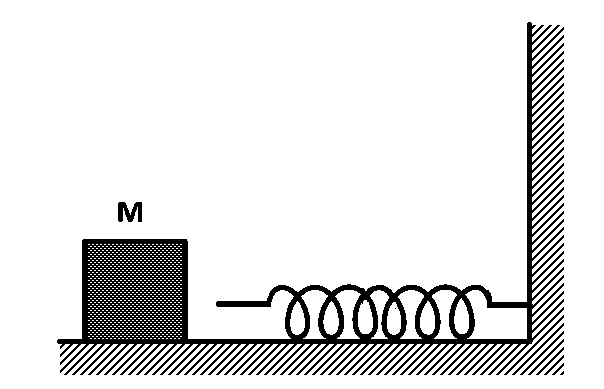
The block of mass $$M$$ moving on the frictionless horizontal surface collides with the spring of spring constant $$k$$ and compresses it by length $$L.$$ The maximum momentum of the block after collision is

$${{k{L^2}} \over {2M}}$$
$$\sqrt {Mk} \,\,L$$
$${{M{L^2}} \over k}$$
Zero
Explanation
Elastic energy stored in the spring = $${1 \over 2}k{L^2}$$
And kinetic energy of the block = $${1 \over 2}M{v^2}$$
$$\therefore$$ $${1 \over 2}M{v^2} = {1 \over 2}k{L^2}$$
$$ \Rightarrow v = \sqrt {{k \over M}} .L$$
$$\therefore$$ Momentum $$ = M \times v = M \times \sqrt {{k \over M}} .L = \sqrt {kM} .L$$
And kinetic energy of the block = $${1 \over 2}M{v^2}$$
$$\therefore$$ $${1 \over 2}M{v^2} = {1 \over 2}k{L^2}$$
$$ \Rightarrow v = \sqrt {{k \over M}} .L$$
$$\therefore$$ Momentum $$ = M \times v = M \times \sqrt {{k \over M}} .L = \sqrt {kM} .L$$
Comments (0)


