JEE MAIN - Physics (2005 - No. 10)
Two concentric coils each of radius equal to $$2$$ $$\pi $$ $$cm$$ are placed at right angles to each other. $$3$$ ampere and $$4$$ ampere are the currents flowing in each coil respectively . The magnetic induction in Weber / $${m^2}$$ at the center of the coils will be
$$\left( {\mu = 4\pi \times {{10}^{ - 7}}Wb/A.m} \right)$$
$$\left( {\mu = 4\pi \times {{10}^{ - 7}}Wb/A.m} \right)$$
$${10^{ - 5}}$$
$$12 \times {10^{ - 5}}$$
$$7 \times {10^{ - 5}}$$
$$5 \times {10^{ - 5}}$$
Explanation
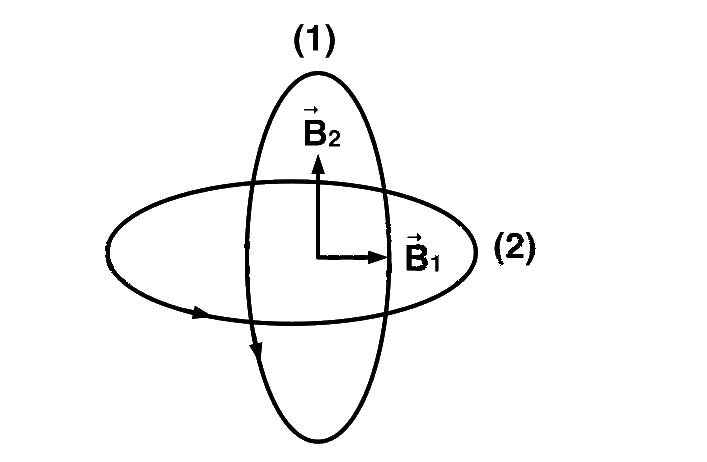
The magnetic field due to circular coil $$1$$ and $$2$$ are
$${B_1} = {{{\mu _0}{i_1}} \over {2r}} = {{{\mu _0}{i_1}} \over {2\left( {2\pi \times {{10}^{ - 2}}} \right)}}$$
$$ = {{{\mu _0} \times 3 \times {{10}^2}} \over {4\pi }}$$
$${B_2} = {{{\mu _0}{i_2}} \over {2\left( {2\pi \times {{10}^{ - 2}}} \right)}} = {{{\mu _0} \times 4 \times {{10}^2}} \over {4\pi }}$$
$$B = \sqrt {B_1^2 + B_2^2} = {{{\mu _0}} \over {4\pi }}.5 \times {10^2}$$
$$ \Rightarrow B = {10^{ - 7}} \times 5 \times {10^2}$$
$$ \Rightarrow B = 5 \times {10^{ - 5}}\,Wb/{m^2}$$
Comments (0)


