JEE MAIN - Physics (2004 - No. 60)
The bob of a simple pendulum executes simple harmonic motion in water with a period $$t,$$ while the period of oscillation of the bob is $${t_0}$$ in air. Neglecting frictional force of water and given that the density of the bob is $$\left( {4/3} \right) \times 1000\,\,kg/{m^3}.$$ What relationship between $$t$$ and $${t_0}$$ is true
$$t = 2{t_0}$$
$$t = {t_0}/2$$
$$t = {t_0}$$
$$t = 4{t_0}$$
Explanation
$$t = 2\pi \sqrt {{\ell \over {{g_{eff}}}}} ;\,{t_o}\,\, = 2\pi \sqrt {{\ell \over g}} $$
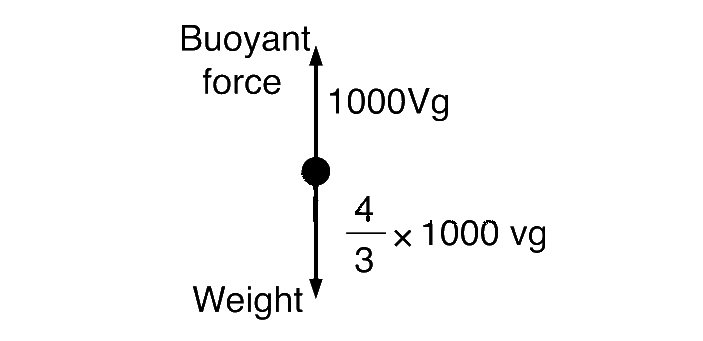
$$m{g_{eff}} = mg - B = my - V \times 100 \times g$$
$$\therefore$$ $${g_{eff}} = g - {{100} \over {\left( {m/v} \right)}}g$$
$$ = g - {{1000} \over {{4 \over 3} \times 1000}}g = {g \over 4}$$
$$\therefore$$ $$t = 2\pi \sqrt {{\ell \over {g/4}}} \,\,\,\,\,\,\,\,\,\,\,t = 2{t_0}$$

$$m{g_{eff}} = mg - B = my - V \times 100 \times g$$
$$\therefore$$ $${g_{eff}} = g - {{100} \over {\left( {m/v} \right)}}g$$
$$ = g - {{1000} \over {{4 \over 3} \times 1000}}g = {g \over 4}$$
$$\therefore$$ $$t = 2\pi \sqrt {{\ell \over {g/4}}} \,\,\,\,\,\,\,\,\,\,\,t = 2{t_0}$$
Comments (0)


