JEE MAIN - Physics (2004 - No. 59)
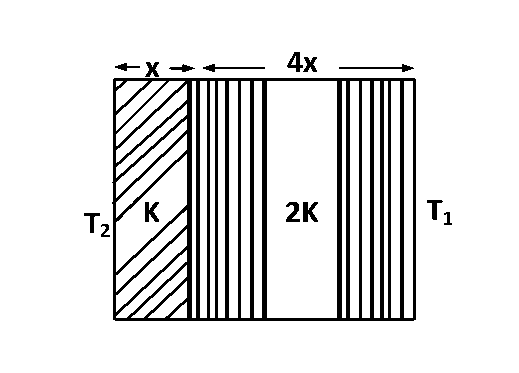
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity $$K$$ and $$2K$$ and thickness $$x$$ and $$4x,$$ respectively, are $${T_2}$$ and $${T_1}\left( {{T_2} > {T_1}} \right).$$ The rate of heat transfer through the slab, in a steady state is $$\left( {{{A\left( {{T_2} - {T_1}} \right)K} \over x}} \right)f,$$ with $$f$$ equal to

$${2 \over 3}$$
$${1 \over 2}$$
$$1$$
$${1 \over 3}$$
Explanation
The thermal resistance
$${x \over {KA}} + {{4x} \over {2KA}} = {{3x} \over {KA}}$$
$$\therefore$$ $${{dQ} \over {dt}} = {{\Delta T} \over {{{3x} \over {KA}}}} = {{\left( {{T_2} - {T_1}} \right)KA} \over {3x}}$$
$$ = {1 \over 3}\left\{ {{{A\left( {{T_2} - {T_1}} \right)K} \over x}} \right\}$$
$$\therefore$$ $$f = {1 \over 3}$$
$${x \over {KA}} + {{4x} \over {2KA}} = {{3x} \over {KA}}$$
$$\therefore$$ $${{dQ} \over {dt}} = {{\Delta T} \over {{{3x} \over {KA}}}} = {{\left( {{T_2} - {T_1}} \right)KA} \over {3x}}$$
$$ = {1 \over 3}\left\{ {{{A\left( {{T_2} - {T_1}} \right)K} \over x}} \right\}$$
$$\therefore$$ $$f = {1 \over 3}$$
Comments (0)


