JEE MAIN - Physics (2004 - No. 38)
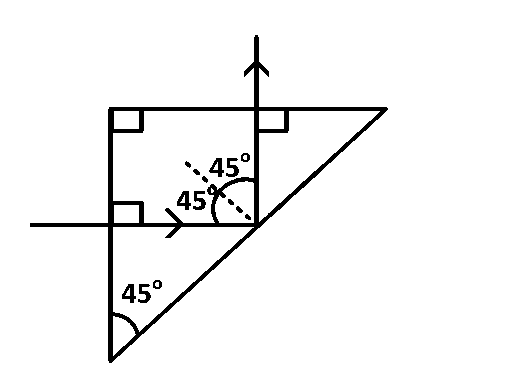
A light ray is incident perpendicularly to one face of a $${90^ \circ }$$ prism and is totally internally reflected at the glass-air interface. If the angle of reflection is $${45^ \circ }$$, we conclude that the refractive index $$n$$

$$n > {1 \over {\sqrt 2 }}$$
$$n > \sqrt 2 $$
$$n < {1 \over {\sqrt 2 }}$$
$$n < \sqrt 2 $$
Explanation
The incident angle is $${45^ \circ }$$
Incident angle $$ > $$ critical angle, $$i > {i_c}$$
$$\therefore$$ $$\sin i > \sin {i_c}$$ or $$\sin \,45\, > \sin \,{i_c},$$ $$\sin {i_c} = {1 \over n}$$
$$\therefore$$ $$\sin \,{45^ \circ } > {1 \over n}$$ or $${1 \over {\sqrt 2 }} > {1 \over n} \Rightarrow n > \sqrt 2 $$
Incident angle $$ > $$ critical angle, $$i > {i_c}$$
$$\therefore$$ $$\sin i > \sin {i_c}$$ or $$\sin \,45\, > \sin \,{i_c},$$ $$\sin {i_c} = {1 \over n}$$
$$\therefore$$ $$\sin \,{45^ \circ } > {1 \over n}$$ or $${1 \over {\sqrt 2 }} > {1 \over n} \Rightarrow n > \sqrt 2 $$
Comments (0)


