JEE MAIN - Physics (2004 - No. 13)
Four charges equal to -$$Q$$ are placed at the four corners of a square and a charge $$q$$ is at its center. If the system is in equilibrium the value of $$q$$ is
$$ - {Q \over 2}\left( {1 + 2\sqrt 2 } \right)$$
$${Q \over 4}\left( {1 + 2\sqrt 2 } \right)$$
$$ - {Q \over 4}\left( {1 + 2\sqrt 2 } \right)$$
$${Q \over 2}\left( {1 + 2\sqrt 2 } \right)$$
Explanation
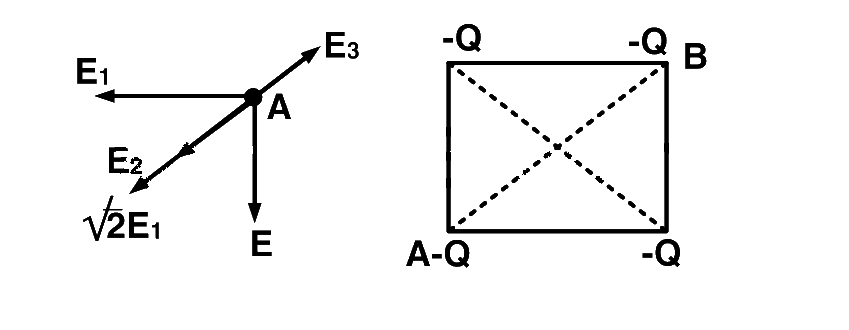
Net field at A should be zero
$$\sqrt 2 \,{E_1} + {E_2} = {E_3}$$
$$\therefore$$ $${{kQ \times \sqrt 2 } \over {{a^2}}} + {{kQ} \over {\left( {\sqrt 2 a} \right)}} = {{kq} \over {{{\left( {{a \over {\sqrt 2 }}} \right)}^2}}}$$
$$ \Rightarrow {{Q\sqrt 2 } \over 1} + {Q \over 2} = 2q$$
$$ \Rightarrow q = {Q \over 4}\left( {2\sqrt 2 + 1} \right).$$
Comments (0)


