JEE MAIN - Physics (2003 - No. 30)
Let $$\overrightarrow F $$ be the force acting on a particle having position vector $$\overrightarrow r ,$$ and $$\overrightarrow \tau $$ be the torque of this force about the origin. Then
$$\overrightarrow {r.} \overrightarrow \tau = 0\,\,$$ and $$\overrightarrow {F.} \overrightarrow \tau \ne 0\,\,$$
$$\overrightarrow {r.} \vec \tau \ne 0{\mkern 1mu} {\mkern 1mu} $$ and $$\overrightarrow {F.} \overrightarrow \tau = 0\,\,$$
$$\overrightarrow {r.} \vec \tau \ne 0{\mkern 1mu} $$ and $$\overrightarrow {F.} \overrightarrow \tau \ne 0$$
$$\overrightarrow {r.} \vec \tau = 0{\mkern 1mu} $$ and $$\overrightarrow {F.} \overrightarrow \tau = 0\,\,$$
Explanation
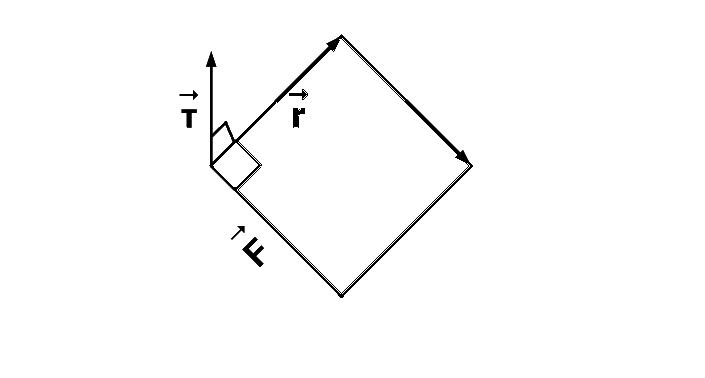
As we know $$\overrightarrow \tau = \overrightarrow r \times \overrightarrow F $$
So the angle between $$\overrightarrow \tau $$ and $$\overrightarrow r $$ is $${90^ \circ }$$ and the angle between $$\overrightarrow t $$ and $$\overrightarrow F $$ is also $${90^ \circ }.$$
We also know that the dot product of two vectors which have an angle of $${90^ \circ }$$ between them is zero.
$$\therefore$$ $$\overrightarrow {r.} \vec \tau = 0{\mkern 1mu} $$ and $$\overrightarrow {F.} \overrightarrow \tau = 0\,\,$$
Therefore $$(d)$$ is the correct option.
Comments (0)


