JEE MAIN - Physics (2003 - No. 26)
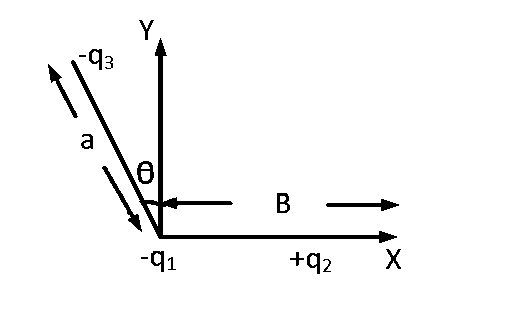
Three charges $$ - {q_1}, + {q_2}$$ and $$ - {q_3}$$ are placed as shown in the figure. The $$x$$-component of the force on $$ - {q_1}$$ is proportional to

$${{{q_2}} \over {{b^2}}} - {{{q_3}} \over {{a^2}}}\cos \theta $$
$${{{q_2}} \over {{b^2}}} + {{{q_3}} \over {{a^2}}}\sin \theta $$
$${{{q_2}} \over {{b^2}}} + {{{q_3}} \over {{a^2}}}\cos \theta $$
$${{{q_2}} \over {{b^2}}} - {{{q_3}} \over {{a^2}}}sin\theta $$
Explanation

Force on charge $${q_1}$$ due to $${q_2}$$ is $${F_{12}} = k{{{q_1}{q_2}} \over {{b^2}}}$$
Force on charge $${q_1}$$ due to $${q_3}$$ is $${F_{13}} = k{{{q_1}{q_3}} \over {{a^2}}}$$
The $$X$$-component of the force $$\left( {{F_x}} \right)$$ on
$$q{}_1$$ is $${F_{12}} + {F_{13}}$$ $$\sin \theta $$
$$\therefore$$ $${F_x} = k{{{q_1}{q_2}} \over {{b^2}}} + k{{{q_1}{q_2}} \over {{a^2}}}\sin \theta $$
$$\therefore$$ $${F_x} \propto {{{q_2}} \over {{b^2}}} + {{{q_3}} \over {{a^2}}}\sin \theta $$
Comments (0)


