JEE MAIN - Physics (2003 - No. 15)
A particle of charge $$ - 16 \times {10^{ - 18}}$$ coulomb moving with velocity $$10m{s^{ - 1}}$$ along the $$x$$-axis enters a region where a magnetic field of induction $$B$$ is along the $$y$$-axis, and an electric field of magnitude $${10^4}V/m$$ is along the negative $$z$$-axis. If the charged particle continues moving along the $$x$$-axis, the magnitude of $$B$$ is
$${10^3}Wb/{m^2}$$
$${10^5}Wb/{m^2}$$
$${10^{16}}Wb/{m^2}$$
$${10^{ - 3}}Wb/{m^2}$$
Explanation
The situation is shown in the figure.
$${F_E} = $$ Force due to electric field
$${F_B} = $$ Force due to magnetic field
It is given that the charged particle remains moving along $$X$$-axis (i.e. undeviated).
Therefore $${F_B} = {F_E}$$
$$ \Rightarrow qvB = qE$$
$$ \Rightarrow B = {E \over v} = {{{{10}^4}} \over {10}}$$
$$ = {10^3}\,\,weber/{m^2}$$
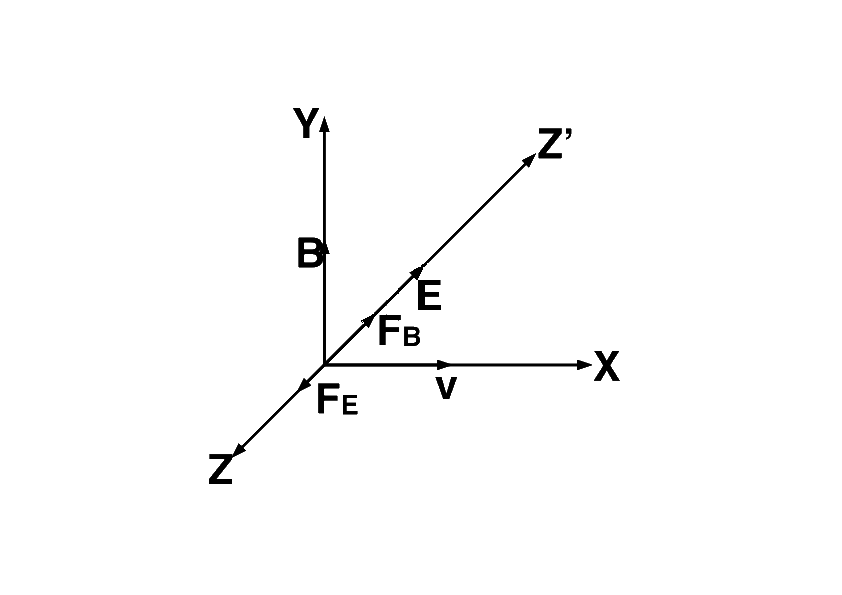
$${F_E} = $$ Force due to electric field
$${F_B} = $$ Force due to magnetic field
It is given that the charged particle remains moving along $$X$$-axis (i.e. undeviated).
Therefore $${F_B} = {F_E}$$
$$ \Rightarrow qvB = qE$$
$$ \Rightarrow B = {E \over v} = {{{{10}^4}} \over {10}}$$
$$ = {10^3}\,\,weber/{m^2}$$

Comments (0)


