JEE MAIN - Physics (2002 - No. 59)
Two forces are such that the sum of their magnitudes is $$18$$ $$N$$ and their resultant is $$12$$ $$N$$ which is perpendicular to the smaller force. Then the magnitudes of the forces are
$$12N,$$ $$6N$$
$$13N,$$ $$5N$$
$$10N,$$ $$8N$$
$$16N$$, $$2N.$$
Explanation
Let the two forces be $${F_1}$$ and $${F_2}$$ and let $${F_2}$$ is smaller than $$ {F_1} $$ and assume $$R$$ is the resultant force.
Given $${F_1} + {F_2} = 18$$ $$\,\,\,\,\,\,$$ ....$$(i)$$
From the right angle triangle, $$F_2^2 + {R^2} = F_1^2$$
or $$F_1^2 - F_2^2 = {R^2}$$
or $$\left( {{F_1} + {F_2}} \right)$$$$\left( {{F_1} - {F_2}} \right)$$ = $${R^2}$$
or $$\left( {18} \right)\left( {{F_1} - {F_2}} \right)$$ = $${\left( {12} \right)^2}$$ = 144
or $$\left( {{F_1} - {F_2}} \right) = 8$$ $$\,\,\,\,\,\,$$ ....$$(ii)$$
By solving equation $$(i)$$ and $$(ii)$$ we get,
$${{F_1} = 13\,N}$$ and $${{F_2} = 5\,N}$$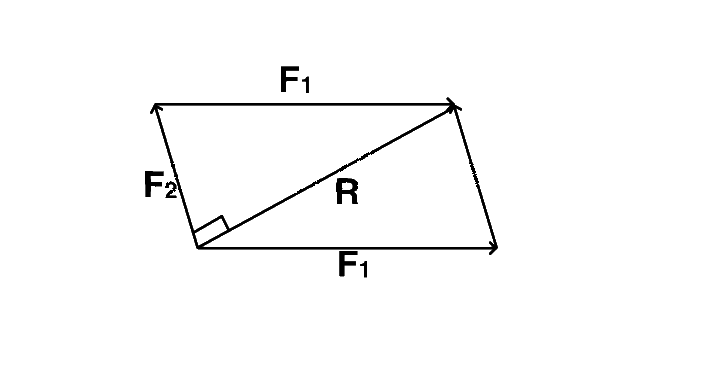
Given $${F_1} + {F_2} = 18$$ $$\,\,\,\,\,\,$$ ....$$(i)$$
From the right angle triangle, $$F_2^2 + {R^2} = F_1^2$$
or $$F_1^2 - F_2^2 = {R^2}$$
or $$\left( {{F_1} + {F_2}} \right)$$$$\left( {{F_1} - {F_2}} \right)$$ = $${R^2}$$
or $$\left( {18} \right)\left( {{F_1} - {F_2}} \right)$$ = $${\left( {12} \right)^2}$$ = 144
or $$\left( {{F_1} - {F_2}} \right) = 8$$ $$\,\,\,\,\,\,$$ ....$$(ii)$$
By solving equation $$(i)$$ and $$(ii)$$ we get,
$${{F_1} = 13\,N}$$ and $${{F_2} = 5\,N}$$

Comments (0)


