JEE MAIN - Physics (2002 - No. 20)
A conducting square loop of side $$L$$ and resistance $$R$$ moves in its plane with a uniform velocity $$v$$ perpendicular to one of its sides. A magnetic induction $$B$$ constant in time and space, pointing perpendicular and into the plane at the loop exists everywhere with half the loop outside the field, as shown in figure. The induced $$emf$$ is
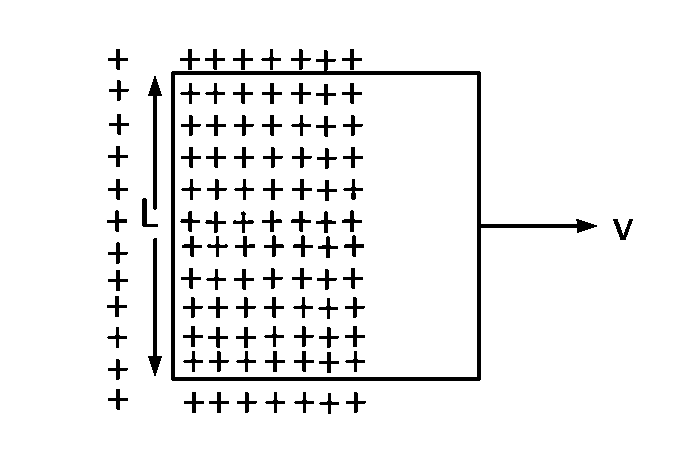

zero
$$RvB$$
$$vBL/R$$
$$vBL$$
Explanation
The induced $$emf$$ is
$$e = {{ - d\phi } \over {dt}} = - {{d\left( {\overrightarrow B .\overrightarrow A } \right)} \over {dt}}$$
$$ = {{ - d\left( {BA\cos {0^ \circ }} \right)} \over {dt}}$$
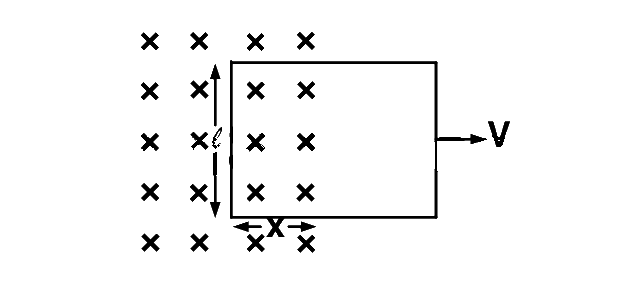
$$\therefore$$ $$e = - B{{dA} \over {dt}} = - B{{d\left( {\ell \times x} \right)} \over {dt}}$$
$$ = - B\ell {{dx} \over {dt}} = - B\ell v$$
$$e = {{ - d\phi } \over {dt}} = - {{d\left( {\overrightarrow B .\overrightarrow A } \right)} \over {dt}}$$
$$ = {{ - d\left( {BA\cos {0^ \circ }} \right)} \over {dt}}$$

$$\therefore$$ $$e = - B{{dA} \over {dt}} = - B{{d\left( {\ell \times x} \right)} \over {dt}}$$
$$ = - B\ell {{dx} \over {dt}} = - B\ell v$$
Comments (0)


