JEE MAIN - Physics (2002 - No. 12)
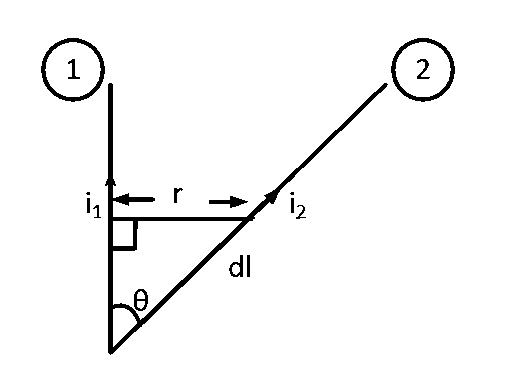
Wires $$1$$ and $$2$$ carrying currents $$i{}_1$$ and $$i{}_2$$ respectively are inclined at an angle $$\theta $$ to each other. What is the force on a small element $$dl$$ of wire $$2$$ at a distance of $$r$$ from wire $$1$$ (as shown in figure) due to the magnetic field of wire $$1$$?

$${{{\mu _0}} \over {2\pi r}}{i_1}{i_2}\,dl\,\tan \,\theta $$
$${{{\mu _0}} \over {2\pi r}}{i_1}{i_2}\,dl\,\sin \,\theta $$
$${{{\mu _0}} \over {2\pi r}}{i_1}{i_2}\,dl\,\cos \,\theta $$
$${{{\mu _0}} \over {4\pi r}}{i_1}{i_2}\,dl\,\sin \,\theta $$
Explanation
Magnetic field due to current in wire $$1$$ at point $$P$$ distant $$r$$ from the wire is
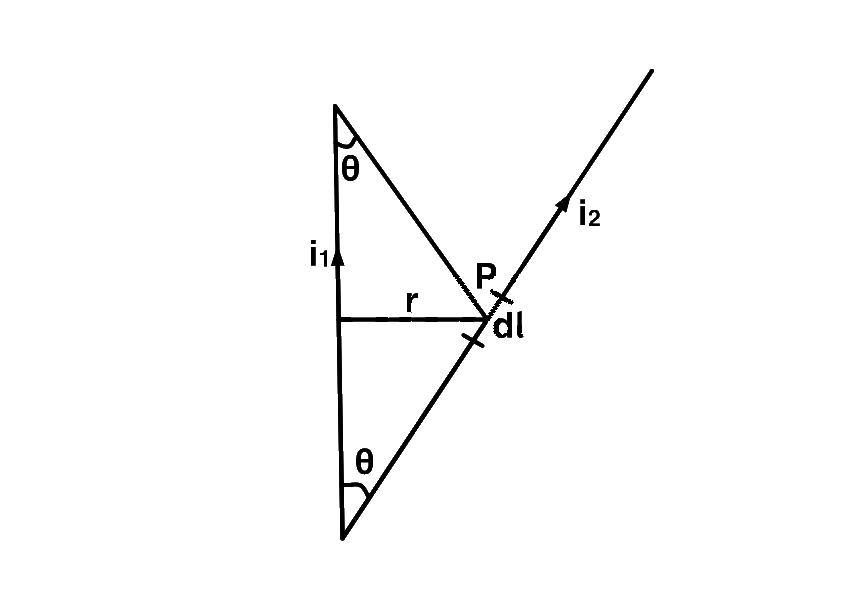
$$B = {{{\mu _0}} \over {4\pi }}{{{i_1}} \over r}\left[ {\cos \theta + \cos \theta } \right]$$
$$B = {{{\mu _0}} \over {2\pi }}{{{i_1}\cos \theta } \over r}$$ (directed perpendicular to the plane of paper, inwards)
The force exerted due to this magnetic field on current element $${i_2}\,dl$$ is
$$dF = {i_2}\,dl\,B\,\sin \,{90^ \circ }$$
$$\therefore$$ $$dF = {i_2}dl\left[ {{{{\mu _0}} \over {2\pi }}{{{i_1}\cos \theta } \over r}} \right]$$
$$ = {{{\mu _0}} \over {2\pi r}}{i_1}\,{i_2}dl\,\cos \,\theta $$

$$B = {{{\mu _0}} \over {4\pi }}{{{i_1}} \over r}\left[ {\cos \theta + \cos \theta } \right]$$
$$B = {{{\mu _0}} \over {2\pi }}{{{i_1}\cos \theta } \over r}$$ (directed perpendicular to the plane of paper, inwards)
The force exerted due to this magnetic field on current element $${i_2}\,dl$$ is
$$dF = {i_2}\,dl\,B\,\sin \,{90^ \circ }$$
$$\therefore$$ $$dF = {i_2}dl\left[ {{{{\mu _0}} \over {2\pi }}{{{i_1}\cos \theta } \over r}} \right]$$
$$ = {{{\mu _0}} \over {2\pi r}}{i_1}\,{i_2}dl\,\cos \,\theta $$
Comments (0)


