JEE MAIN - Mathematics (2012 - No. 5)
Let $$a,b \in R$$ be such that the function $$f$$ given by $$f\left( x \right) = In\left| x \right| + b{x^2} + ax,\,x \ne 0$$ has extreme values at $$x=-1$$ and $$x=2$$
Statement-1 : $$f$$ has local maximum at $$x=-1$$ and at $$x=2$$.
Statement-2 : $$a = {1 \over 2}$$ and $$b = {-1 \over 4}$$
Statement - 1 is false, Statement - 2 is true.
Statement - 1 is true , Statement - 2 is true; Statement - 2 is a correct explanation for Statement - 1.
Statement - 1 is true, Statement - 2 is true; Statement - 2 is not a correct explanation for Statement - 1.
Statement - 1 is true, Statement - 2 is false.
Explanation
Given, $$f\left( x \right) = \ln \left| x \right| + b{x^2} + ax$$
$$\therefore$$ $$f'\left( x \right) = {1 \over x} + 2bx + a$$
At $$x=-1,$$ $$f'\left( x \right) = - 1 - 2b + a = 0$$
$$ \Rightarrow a - 2b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)$$
At $$x=2,$$ $$\,\,f'\left( x \right) = {1 \over 2} + 4b + a = 0$$
$$ \Rightarrow a + 4b = - {1 \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)$$
On solving $$(i)$$ and $$(ii)$$ we get $$a = {1 \over 2},b = - {1 \over 4}$$
Thus, $$f'\left( x \right) = {1 \over x} - {x \over 2} + {1 \over 2} = {{2 - {x^2} + x} \over {2x}}$$
$$ = {{ - {x^2} + x + 2} \over {2x}} = {{ - \left( {{x^2} - x - 2} \right)} \over {2x}} = {{ - \left( {x + 1} \right)\left( {x - 2} \right)} \over {2x}}$$
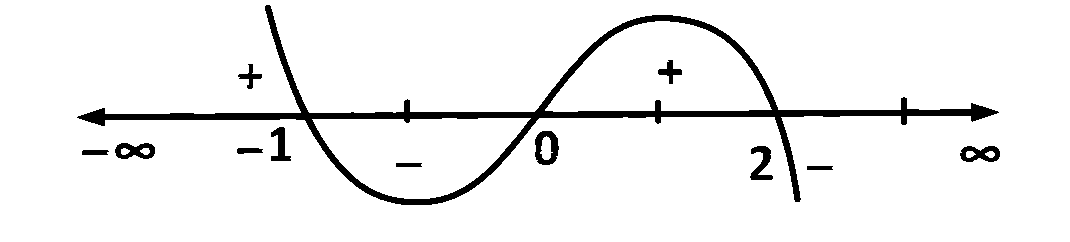
So maximum at $$x=-1,2$$
Hence both the statements are true and statement $$2$$ is a correct explanation for $$1.$$
$$\therefore$$ $$f'\left( x \right) = {1 \over x} + 2bx + a$$
At $$x=-1,$$ $$f'\left( x \right) = - 1 - 2b + a = 0$$
$$ \Rightarrow a - 2b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)$$
At $$x=2,$$ $$\,\,f'\left( x \right) = {1 \over 2} + 4b + a = 0$$
$$ \Rightarrow a + 4b = - {1 \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)$$
On solving $$(i)$$ and $$(ii)$$ we get $$a = {1 \over 2},b = - {1 \over 4}$$
Thus, $$f'\left( x \right) = {1 \over x} - {x \over 2} + {1 \over 2} = {{2 - {x^2} + x} \over {2x}}$$
$$ = {{ - {x^2} + x + 2} \over {2x}} = {{ - \left( {{x^2} - x - 2} \right)} \over {2x}} = {{ - \left( {x + 1} \right)\left( {x - 2} \right)} \over {2x}}$$
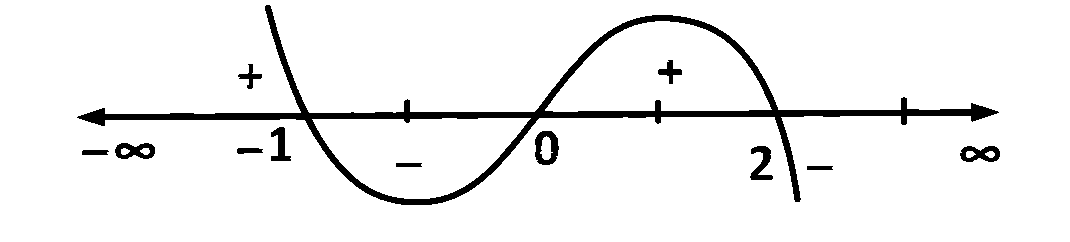
So maximum at $$x=-1,2$$
Hence both the statements are true and statement $$2$$ is a correct explanation for $$1.$$
Comments (0)


