JEE MAIN - Mathematics (2012 - No. 4)
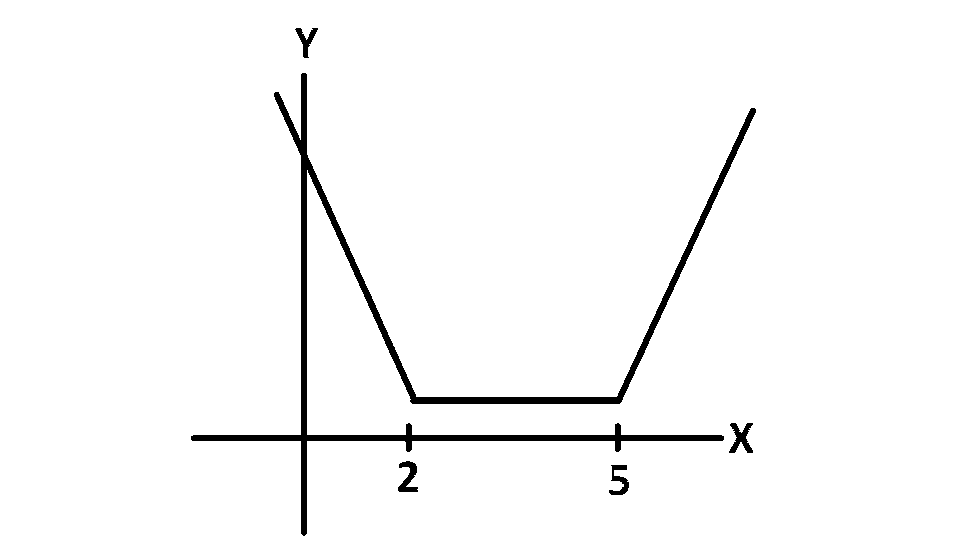
Consider the function, $$f\left( x \right) = \left| {x - 2} \right| + \left| {x - 5} \right|,x \in R$$
Statement - 1 : $$f'\left( 4 \right) = 0$$
Statement - 2 : $$f$$ is continuous in [2, 5], differentiable in (2, 5) and $$f$$(2) = $$f$$(5)
Statement - 1 : $$f'\left( 4 \right) = 0$$
Statement - 2 : $$f$$ is continuous in [2, 5], differentiable in (2, 5) and $$f$$(2) = $$f$$(5)
Statement - 1 is false, statement - 2 is true
Statement - 1 is true, statement - 2 is true; statement - 2 is a correct explanation for statement - 1
Statement - 1 is true, statement - 2 is true; statement - 2 is not a correct explanation for statement - 1
Statement - 1 is true, statement - 2 is false
Explanation
$$f\left( x \right) = \left| {x - 2} \right| = \left\{ {\matrix{
{x - 2\,\,\,,} & {x - 2 \ge 0} \cr
{2 - x\,\,\,,} & {x - 2 \le 0} \cr
} } \right.$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left\{ {\matrix{ {x - 2\,\,\,,} & {x \ge 2} \cr {2 - x\,\,\,,} & {x \le 2} \cr } } \right.$$
Similarly, $$f\left( x \right) = \left| {x - 5} \right| = \left\{ {\matrix{ {x - 5\,\,\,,} & {x \ge 5} \cr {5 - x\,\,\,,} & {x \le 5} \cr } } \right.$$
$$\therefore$$ $$f\left( x \right) = \left| {x - 2} \right| + \left| {x - 5} \right|$$
$$ = \left\{ {x - 2 + 5 - x = 3,2 \le x \le 5} \right\}$$
Thus $$\,\,\,\,\,\,\,\,\,f\left( x \right) = 3,2 \le x \le 5$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f'\left( x \right) = 0,2 < x < 5$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f'\left( 4 \right) = 0$$
$$\therefore$$ Statement $$1$$ is true.
As $$f\left( 2 \right) = 0 + \left| {2 - 5} \right| = 3$$
and $$f\left( 5 \right) = \left| {5 - 2} \right| + 0 = 3$$
$$\therefore$$ Statement - $$2$$ is also true but not a correct explanation for statement $$1.$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left\{ {\matrix{ {x - 2\,\,\,,} & {x \ge 2} \cr {2 - x\,\,\,,} & {x \le 2} \cr } } \right.$$
Similarly, $$f\left( x \right) = \left| {x - 5} \right| = \left\{ {\matrix{ {x - 5\,\,\,,} & {x \ge 5} \cr {5 - x\,\,\,,} & {x \le 5} \cr } } \right.$$
$$\therefore$$ $$f\left( x \right) = \left| {x - 2} \right| + \left| {x - 5} \right|$$
$$ = \left\{ {x - 2 + 5 - x = 3,2 \le x \le 5} \right\}$$
Thus $$\,\,\,\,\,\,\,\,\,f\left( x \right) = 3,2 \le x \le 5$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f'\left( x \right) = 0,2 < x < 5$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f'\left( 4 \right) = 0$$
$$\therefore$$ Statement $$1$$ is true.

As $$f\left( 2 \right) = 0 + \left| {2 - 5} \right| = 3$$
and $$f\left( 5 \right) = \left| {5 - 2} \right| + 0 = 3$$
$$\therefore$$ Statement - $$2$$ is also true but not a correct explanation for statement $$1.$$
Comments (0)


