JEE MAIN - Mathematics (2012 - No. 22)
Let $$ABCD$$ be a parallelogram such that $$\overrightarrow {AB} = \overrightarrow q ,\overrightarrow {AD} = \overrightarrow p $$ and $$\angle BAD$$ be an acute angle. If $$\overrightarrow r $$ is the vector that coincide with the altitude directed from the vertex $$B$$ to the side $$AD,$$ then $$\overrightarrow r $$ is given by :
$$\overrightarrow r = 3\overrightarrow q - {{3\left( {\overrightarrow p .\overrightarrow q } \right)} \over {\left( {\overrightarrow p .\overrightarrow p } \right)}}\overrightarrow p $$
$$\overrightarrow r = - \overrightarrow q + {{\left( {\overrightarrow p .\overrightarrow q } \right)} \over {\left( {\overrightarrow p .\overrightarrow p } \right)}}\overrightarrow p $$
$$\vec r = \vec q - {{\left( {\vec p.\vec q} \right)} \over {\left( {\vec p.\vec p} \right)}}\vec p$$
$$\overrightarrow r = - 3\overrightarrow q - {{3\left( {\overrightarrow p .\overrightarrow q } \right)} \over {\left( {\overrightarrow p .\overrightarrow p } \right)}}$$
Explanation
Let $$ABCD$$ be a parallelogram such that
$$\overrightarrow {AB} = \overrightarrow q ,\overrightarrow {AD} = \overrightarrow p $$ and $$\angle BAD$$ be an acute angle.
We have
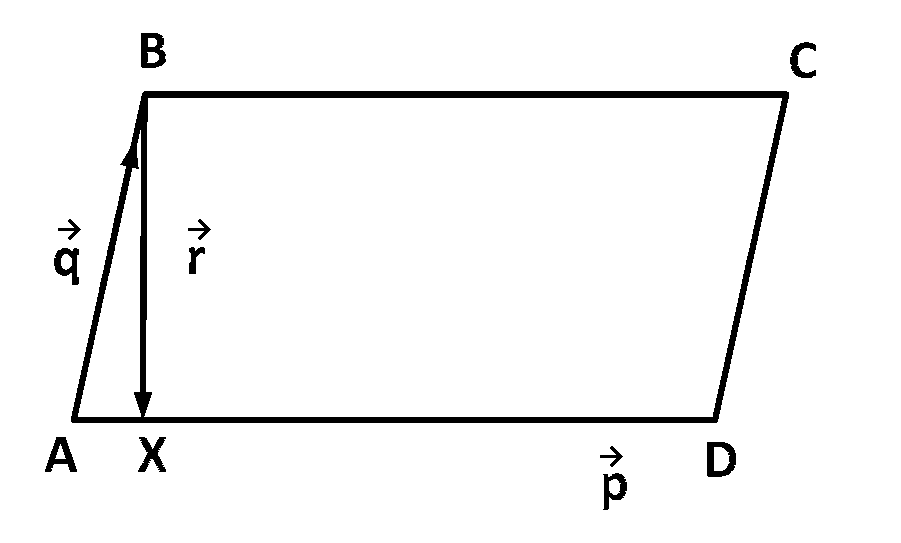
$$\overrightarrow {AX} = \left( {{{\overrightarrow p .\overrightarrow q } \over {\left| {\overrightarrow p } \right|}}} \right)\left( {{{\overrightarrow p } \over {\left| {\overrightarrow p } \right|}}} \right) = {{\overrightarrow p .\overrightarrow q } \over {{{\left| {\overrightarrow p } \right|}^2}}}\overrightarrow p $$
Let $$\overrightarrow r = \overrightarrow {BX} = \overrightarrow {BA} + \overrightarrow {AX} $$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \overrightarrow q + {{\overrightarrow p .\overrightarrow q } \over {{{\left| {\overrightarrow p } \right|}^2}}}\overrightarrow p $$
$$\overrightarrow {AB} = \overrightarrow q ,\overrightarrow {AD} = \overrightarrow p $$ and $$\angle BAD$$ be an acute angle.
We have

$$\overrightarrow {AX} = \left( {{{\overrightarrow p .\overrightarrow q } \over {\left| {\overrightarrow p } \right|}}} \right)\left( {{{\overrightarrow p } \over {\left| {\overrightarrow p } \right|}}} \right) = {{\overrightarrow p .\overrightarrow q } \over {{{\left| {\overrightarrow p } \right|}^2}}}\overrightarrow p $$
Let $$\overrightarrow r = \overrightarrow {BX} = \overrightarrow {BA} + \overrightarrow {AX} $$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \overrightarrow q + {{\overrightarrow p .\overrightarrow q } \over {{{\left| {\overrightarrow p } \right|}^2}}}\overrightarrow p $$
Comments (0)


