JEE MAIN - Mathematics (2012 - No. 16)
The length of the diameter of the circle which touches the $$x$$-axis at the point $$(1, 0)$$ and passes through the point $$(2, 3)$$ is :
$${{10} \over 3}$$
$${{3} \over 5}$$
$${{6} \over 5}$$
$${{5} \over 3}$$
Explanation
Let center of the circle be $$\left( {1,h} \right)$$
$$\left[ {\,\,} \right.$$ as circle touches $$x$$-axis at $$\left. {\left( {1,0} \right)\,\,} \right]$$
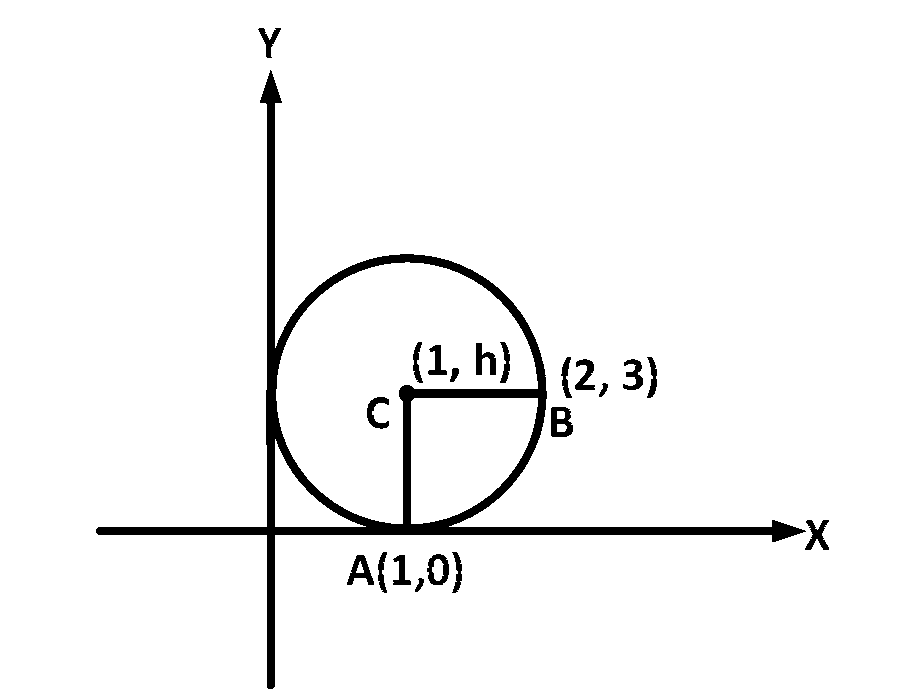
Let the circle passes through the point $$B(2,3)$$
$$\therefore$$ $$CA=CB$$ (radius)
$$ \Rightarrow C{A^2} = C{B^2}$$
$$ \Rightarrow {\left( {1 - 1} \right)^2} + \left( {h - 0} \right){}^2 = {\left( {1 - 2} \right)^2} + {\left( {h - 3} \right)^2}$$
$$ \Rightarrow {h^2} = 1 + {h^2} + 9 - 6h$$
$$ \Rightarrow h = {{10} \over 6} = {5 \over 3}$$
Thus, diameter is $$2h = {{10} \over 3}.$$
$$\left[ {\,\,} \right.$$ as circle touches $$x$$-axis at $$\left. {\left( {1,0} \right)\,\,} \right]$$

Let the circle passes through the point $$B(2,3)$$
$$\therefore$$ $$CA=CB$$ (radius)
$$ \Rightarrow C{A^2} = C{B^2}$$
$$ \Rightarrow {\left( {1 - 1} \right)^2} + \left( {h - 0} \right){}^2 = {\left( {1 - 2} \right)^2} + {\left( {h - 3} \right)^2}$$
$$ \Rightarrow {h^2} = 1 + {h^2} + 9 - 6h$$
$$ \Rightarrow h = {{10} \over 6} = {5 \over 3}$$
Thus, diameter is $$2h = {{10} \over 3}.$$
Comments (0)


