JEE MAIN - Mathematics (2011 - No. 8)
If $$C$$ and $$D$$ are two events such that $$C \subset D$$ and $$P\left( D \right) \ne 0,$$ then the correct statement among the following is :
$$P\left( {{C \over D}} \right)$$$$ \ge P\left( C \right)$$
$$P\left( {{C \over D}} \right)$$$$ < P\left( C \right)$$
$$P\left( {{C \over D}} \right)$$$$ = {{P\left( D \right)} \over {P\left( C \right)}}$$
$$P\left( {{C \over D}} \right)$$$$ = P\left( C \right)$$
Explanation
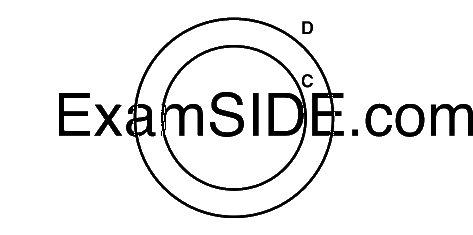
Given that $$C \subset D$$ means $$C$$ is present entirely inside $$D$$. Which is shown below.
$$P\left( {{C \over D}} \right)$$ = $${{P\left( {C \cap D} \right)} \over {P\left( D \right)}}$$ = $${{P\left( C \right)} \over {P\left( D \right)}}$$
As $$C \cap D$$ means common part of events C and D which is equal to C.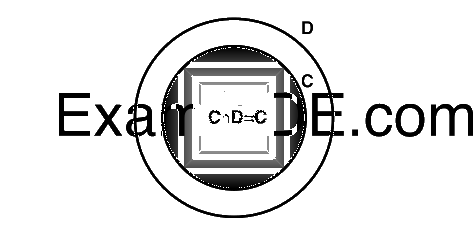
$$0 \le P\left( D \right) \le 1$$
$$\therefore$$ $${{P\left( C \right)} \over {P\left( D \right)}} \ge P\left( C \right)$$
Note: Here we are dividing with $${P\left( D \right)}$$ which is $$ \le 1$$ and $$ \ge 0$$, as we know on dividing with a number n in the range $$0 \le n \le 1$$ we get always more than or equal to the original number.

$$P\left( {{C \over D}} \right)$$ = $${{P\left( {C \cap D} \right)} \over {P\left( D \right)}}$$ = $${{P\left( C \right)} \over {P\left( D \right)}}$$
As $$C \cap D$$ means common part of events C and D which is equal to C.

$$0 \le P\left( D \right) \le 1$$
$$\therefore$$ $${{P\left( C \right)} \over {P\left( D \right)}} \ge P\left( C \right)$$
Note: Here we are dividing with $${P\left( D \right)}$$ which is $$ \le 1$$ and $$ \ge 0$$, as we know on dividing with a number n in the range $$0 \le n \le 1$$ we get always more than or equal to the original number.
Comments (0)


