JEE MAIN - Mathematics (2010 - No. 9)
The area bounded by the curves $$y = \cos x$$ and $$y = \sin x$$ between the ordinates $$x=0$$ and $$x = {{3\pi } \over 2}$$ is
$$4\sqrt 2 + 2$$
$$4\sqrt 2 - 1$$
$$4\sqrt 2 + 1$$
$$4\sqrt 2 - 2$$
Explanation
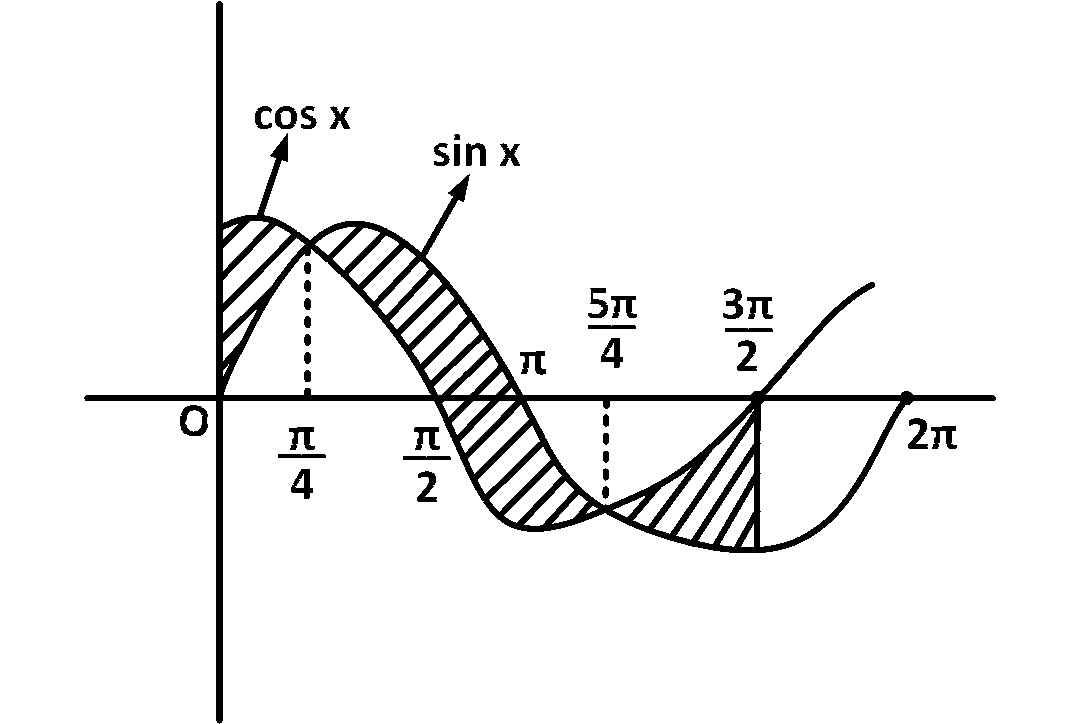
$$\therefore$$ Required area
$$ = \left[ {\int\limits_0^{{\pi \over 4}} {\left( {\cos \,x - \sin x} \right)dx + } } \right.$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\int\limits_{{\pi \over 4}}^{{5\pi \over 4}} {\left( {\sin x - \cos x} \right)dx + } $$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\int\limits_{{5\pi \over 4}}^{{3\pi \over 2}} {\left( {\cos x - \sin x} \right)dx } $$
$$ = 4\sqrt 2 - 2$$
Comments (0)


