The given parabola is $${\left( {y - 2} \right)^2} = x - 1$$

Vertex $$\left( {1,2} \right)$$ and it meets $$x$$-axis at $$\left( {5,0} \right)$$

Also it gives $${y^2} - 4y - x + 5 = 0$$

So, that equation of tangent to the parabola at $$\left( {2,3} \right)$$ is

$$y.3 - 2\left( {y + 3} \right) - {1 \over 2}\left( {x + 2} \right) + 5 = 0$$

or $$x - 2y + 4 = 0$$

which meets $$x$$-axis at $$\left( { - 4,0} \right).$$

In the figure shaded area is the required area.

Let us draw $$PD$$ perpendicular to $$y$$-axis.



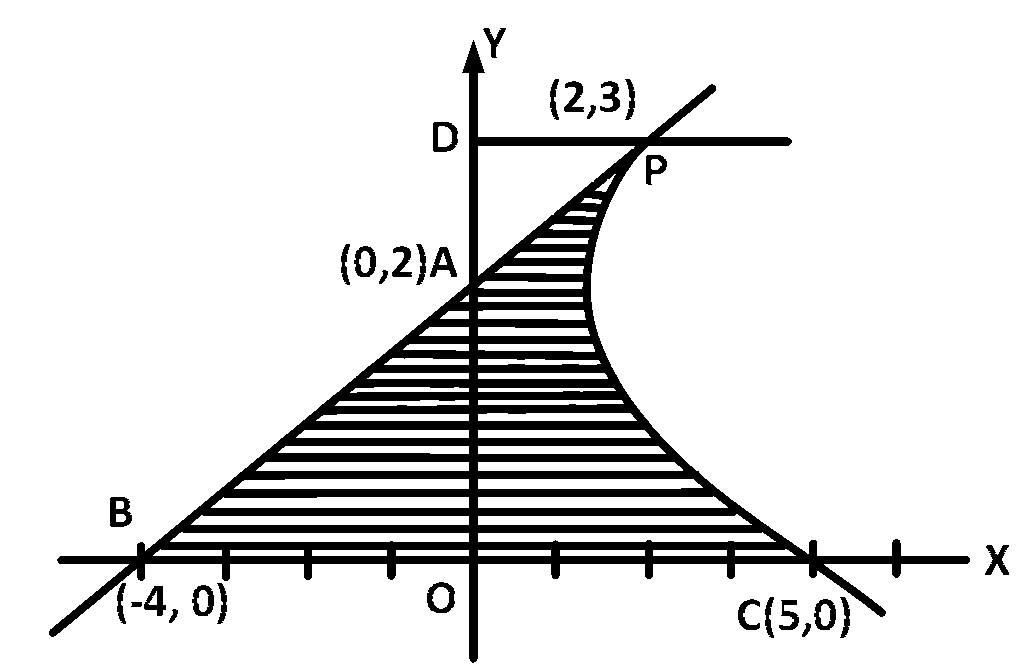
Then required area

$$ = Ar\,\,\Delta BOA + Ar\,\,\left( {OCPD} \right)\, - \,Ar\left( {\Delta APD} \right)$$

$$ = {1 \over 2} \times 4 \times 2 + \int_0^3 {xdy - {1 \over 2}} \times 2 \times 1$$

$$ = 3 + \int_0^3 {{{\left( {y - 2} \right)}^2} + 1\,dy} $$

$$ = 3 + \left[ {{{{{\left( {y - 2} \right)}^3}} \over 3} + y} \right]_0^3$$

$$ = 3 + \left[ {{1 \over 3} + 3 + {8 \over 3}} \right] = 3 + 6 = 9$$ Sq. units