JEE MAIN - Mathematics (2008 - No. 8)
The area of the plane region bounded by the curves $$x + 2{y^2} = 0$$ and $$\,x + 3{y^2} = 1$$ is equal to :
$${5 \over 3}$$
$${1 \over 3}$$
$${2 \over 3}$$
$${4 \over 3}$$
Explanation
$$x + 2{y^2} = 0 \Rightarrow {y^2} = - {x \over 2}$$
$$\left[ {} \right.$$ Left handed parabola with vertex at $$\left( {0,0} \right)$$ $$\left. {} \right]$$
$$x + 3{y^2} = 1 \Rightarrow {y^2} = - {1 \over 3}\left( {x - 1} \right)$$
$$\left[ {} \right.$$ Left handed parabola with vertex at $$\left( {1,0} \right)$$ $$\left. {} \right]$$
Solving the two equations we get the points of intersection
as $$\left( { - 2,1} \right),\left( { - 2, - 1} \right)$$
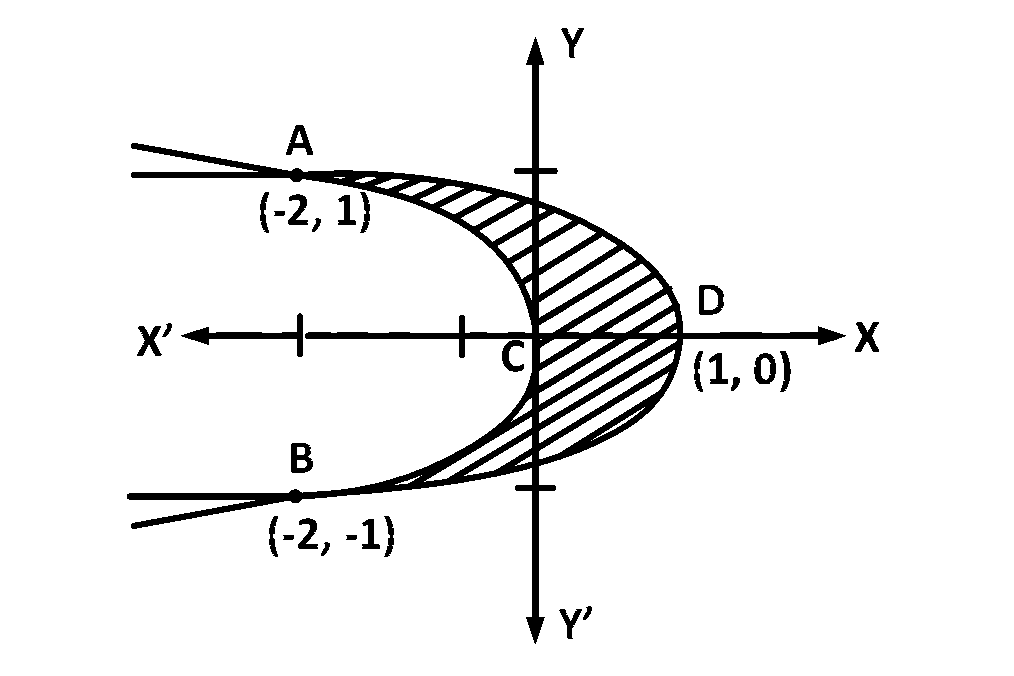
The required area is $$ACBDA,$$ given by
$$ = \left| {\int\limits_{ - 1}^1 {\left( {1 - 3{y^2} - 2{y^2}} \right)dy} } \right|$$
$$ = \left| {\left[ {y - {{5{y^3}} \over 3}} \right]_{ - 1}^1} \right|$$
$$ = \left| {\left( {1 - {5 \over 3}} \right) - \left( { - 1 + {5 \over 3}} \right)} \right|$$
$$ = 2 \times {2 \over 3} = {4 \over 3}\,\,$$ sq. units.
$$\left[ {} \right.$$ Left handed parabola with vertex at $$\left( {0,0} \right)$$ $$\left. {} \right]$$
$$x + 3{y^2} = 1 \Rightarrow {y^2} = - {1 \over 3}\left( {x - 1} \right)$$
$$\left[ {} \right.$$ Left handed parabola with vertex at $$\left( {1,0} \right)$$ $$\left. {} \right]$$
Solving the two equations we get the points of intersection
as $$\left( { - 2,1} \right),\left( { - 2, - 1} \right)$$

The required area is $$ACBDA,$$ given by
$$ = \left| {\int\limits_{ - 1}^1 {\left( {1 - 3{y^2} - 2{y^2}} \right)dy} } \right|$$
$$ = \left| {\left[ {y - {{5{y^3}} \over 3}} \right]_{ - 1}^1} \right|$$
$$ = \left| {\left( {1 - {5 \over 3}} \right) - \left( { - 1 + {5 \over 3}} \right)} \right|$$
$$ = 2 \times {2 \over 3} = {4 \over 3}\,\,$$ sq. units.
Comments (0)


