The given circle is $${x^2} + {y^2} + 2x + 4y - 3 = 0$$



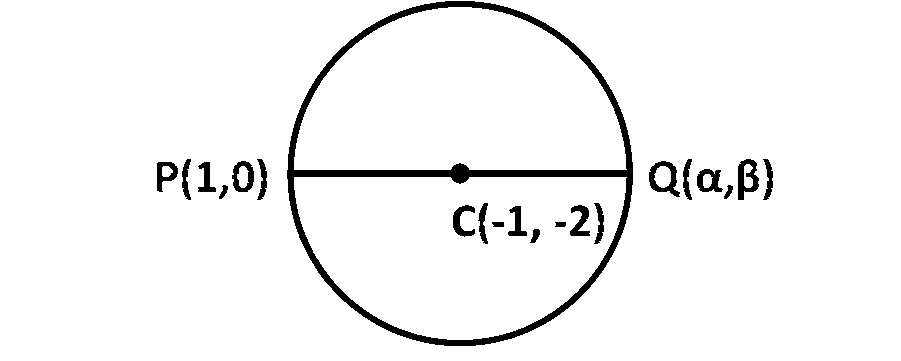
Center $$(-1,-2)$$

Let $$Q$$ $$\left( {\alpha ,\beta } \right)$$ be the point diametrically opposite to the point $$P(1,0),$$

then $${{1 + \alpha } \over 2} = - 1$$ and $${{0 + \beta } \over 2} = - 2$$

$$ \Rightarrow \alpha = - 3,\beta = - 4,$$ So, $$Q$$ is $$\left( { - 3, - 4} \right)$$