JEE MAIN - Mathematics (2007 - No. 3)
Let $$f:R \to R$$ be a function defined by
$$f(x) = \min \left\{ {x + 1,\left| x \right| + 1} \right\}$$, then which of the following is true?
$$f(x) = \min \left\{ {x + 1,\left| x \right| + 1} \right\}$$, then which of the following is true?
$$f(x)$$ is differentiale everywhere
$$f(x)$$ is not differentiable at x = 0
$$f(x) > 1$$ for all $$x \in R$$
$$f(x)$$ is not differentiable at x = 1
Explanation
$$f\left( x \right) = \min \left\{ {x + 1,\left| x \right| + 1} \right\}$$
$$ \Rightarrow f\left( x \right) = x + 1\,\forall \,x \in R$$
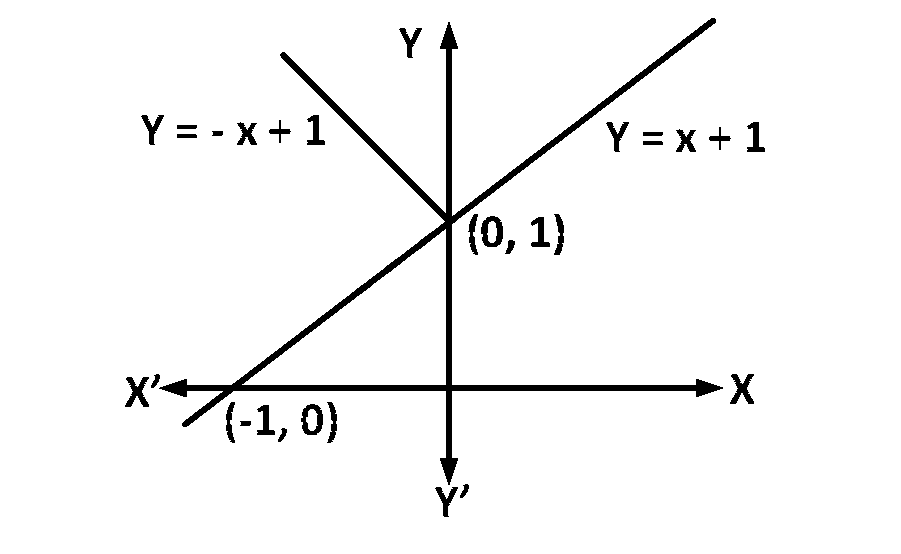
Hence, $$f(x)$$ is differentiable everywhere for all $$x \in R.$$
$$ \Rightarrow f\left( x \right) = x + 1\,\forall \,x \in R$$

Hence, $$f(x)$$ is differentiable everywhere for all $$x \in R.$$
Comments (0)


