JEE MAIN - Mathematics (2006 - No. 6)
A triangular park is enclosed on two sides by a fence and on the third side by a straight river bank. The two sides having fence are of same length $$x$$. The maximum area enclosed by the park is
$${3 \over 2}{x^2}$$
$$\sqrt {{{{x^3}} \over 8}} $$
$${1 \over 2}{x^2}$$
$$\pi {x^2}$$
Explanation
Area $$ = {1 \over 2}{x^2}\,\sin \,\theta $$
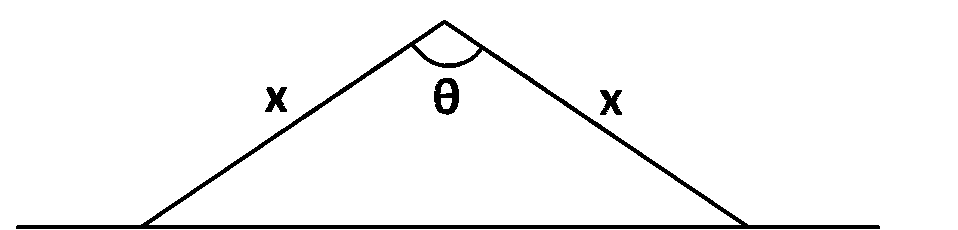
Maximum value of $$\sin \theta $$ is $$1$$ at $$\theta = {\pi \over 2}$$
$${A_{\max }} = {1 \over 2}{x^2}$$

Maximum value of $$\sin \theta $$ is $$1$$ at $$\theta = {\pi \over 2}$$
$${A_{\max }} = {1 \over 2}{x^2}$$
Comments (0)


