JEE MAIN - Mathematics (2005 - No. 49)
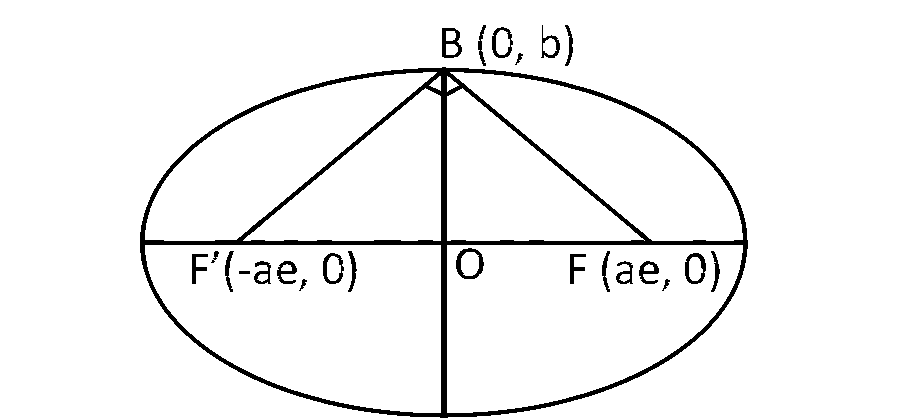
An ellipse has $$OB$$ as semi minor axis, $$F$$ and $$F$$' its focii and theangle $$FBF$$' is a right angle. Then the eccentricity of the ellipse is :
$${1 \over {\sqrt 2 }}$$
$${1 \over 2}$$
$${1 \over 4}$$
$${1 \over {\sqrt 3 }}$$
Explanation
as $$\angle FBF' = {90^ \circ }$$
$$ \Rightarrow F{B^2} + F'{B^2} = FF{'^2}$$
$$\therefore$$ $${\left( {\sqrt {{a^2}{e^2} + {b^2}} } \right)^2} + \left( {\sqrt {{a^2}{e^2} + {b^2}} } \right) = {\left( {2ae} \right)^2}$$
$$ \Rightarrow 2\left( {{a^2}{e^2} + {b^2}} \right) = 4{a^2}{e^2}$$
$$ \Rightarrow {e^2} = {{{b^2}} \over {{a^2}}}$$
Also $${e^2} = 1 - {b^2}/{a^2} = 1 - {e^2}$$
$$ \Rightarrow 2{e^2} = 1,\,\,e = {1 \over {\sqrt 2 }}$$
$$ \Rightarrow F{B^2} + F'{B^2} = FF{'^2}$$
$$\therefore$$ $${\left( {\sqrt {{a^2}{e^2} + {b^2}} } \right)^2} + \left( {\sqrt {{a^2}{e^2} + {b^2}} } \right) = {\left( {2ae} \right)^2}$$
$$ \Rightarrow 2\left( {{a^2}{e^2} + {b^2}} \right) = 4{a^2}{e^2}$$
$$ \Rightarrow {e^2} = {{{b^2}} \over {{a^2}}}$$

Also $${e^2} = 1 - {b^2}/{a^2} = 1 - {e^2}$$
$$ \Rightarrow 2{e^2} = 1,\,\,e = {1 \over {\sqrt 2 }}$$
Comments (0)


