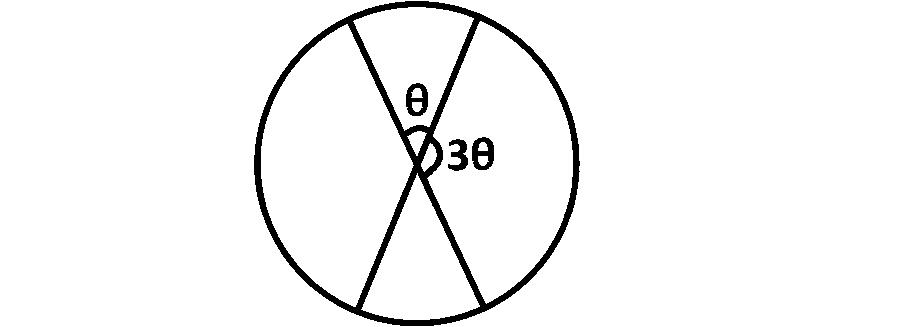
As per question area of one sector $$=3$$ area of another sector

$$ \Rightarrow $$ at center by one sector $$ = 3 \times $$ angle at center by another sector

Let one angle be $$\theta $$ then other $$=30$$

Clearly $$\theta + 3\theta = 180 \Rightarrow \theta = {45^ \circ }$$

$$\therefore$$ Angle between the diameters represented by combined equation

$$a{x^2} + 2\left( {a + b\,\,\,xy} \right) + b{y^2} = 0$$ is $${45^ \circ }$$

$$\therefore$$ Using $$tan$$ $$\theta $$ $$ = {{2\sqrt {{h^2} - ab} } \over {a + b}}$$

we get $$\tan \,{45^ \circ } = {{2\sqrt {{{\left( {a + b} \right)}^2} - ab} } \over {a + b}}$$

$$ \Rightarrow 1 = {{2\sqrt {{a^2} + {b^2} + ab} } \over {a + b}}$$

$$ \Rightarrow {\left( {a + b} \right)^2} = 4\left( {{a^2} + {b^2} + ab} \right)$$

$$ \Rightarrow {a^2} + {b^2} + 2ab = 4{a^2} + 4{b^2} + 4ab$$

$$ \Rightarrow 3{a^2} + 3{b^2} + 2ab = 0$$