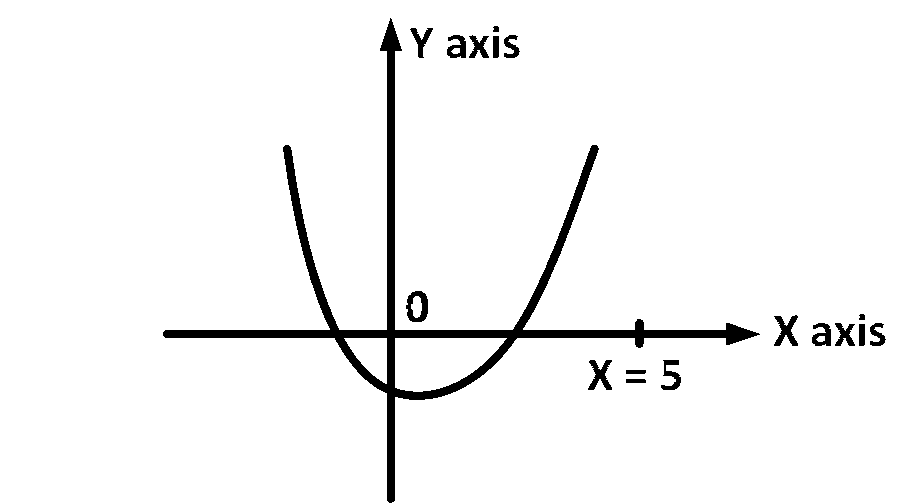
both roots are less than $$5,$$

then $$(i)$$ Discriminant $$ \ge 0$$

$$\left( {ii} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,p\left( 5 \right) > 0$$

$$\left( {iii} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{Sum\,\,of\,\,roots} \over 2} < 5$$

Hence $$\left( i \right)\,\,\,\,\,\,4{k^2} - 4\left( {{k^2} + k - 5} \right) \ge 0$$

$$4{k^2} - 4{k^2} - 4k + 20 \ge 0$$

$$4k \le 20 \Rightarrow k \le 5$$

$$\left( {ii} \right)\,\,\,\,\,f\left( 5 \right) > 0;25 - 10k + {k^2} + k - 5 > 0$$

or $${k^2} - 9k + 20 > 0$$

or $$k\left( {k - 4} \right) - 5\left( {k - 4} \right) > 0$$

or $$\left( {k - 5} \right)\left( {k - 4} \right) > 0$$

$$ \Rightarrow k \in \left( { - \infty ,4} \right) \cup \left( { - \infty ,5} \right)$$

$$\left( {iii} \right)\,\,\,\,\,\,{{Sum\,\,of\,\,roots} \over 2}$$

$$ = - {b \over {2a}} = {{2k} \over 2} < 5$$

The intersection of $$(i)$$, $$(ii)$$ & $$(iii)$$ gives

$$k \in \left( { - \infty ,4} \right).$$