JEE MAIN - Mathematics (2005 - No. 38)
If $$\,\omega = {z \over {z - {1 \over 3}i}}\,$$ and $$\left| \omega \right| = 1$$, then $$z$$ lies on :
an ellipse
a circle
a straight line
a parabola
Explanation
Given $$\,\omega = {z \over {z - {1 \over 3}i}}\,$$ and $$\left| \omega \right| = 1$$
$$\therefore$$ $${{\left| z \right|} \over {\left| {z - {1 \over {\sqrt 3 }}i} \right|}} = \left| \omega \right|$$
$$ \Rightarrow $$ $${{\left| z \right|} \over {\left| {z - {1 \over {\sqrt 3 }}i} \right|}} = 1$$
$$ \Rightarrow $$ $$\left| z \right| = \left| {z - {1 \over {\sqrt 3 }}i} \right|$$ ..........equation (1)
$$\left| z \right|$$ represent distance of $$z$$ from point (0, 0) and
$$\left| {z - {1 \over {\sqrt 3 }}i} \right|$$ represent distance of $$z$$ from point $$\left( {0,{1 \over {\sqrt 3 }}} \right)$$.
According to the equation (1) the distance of $$z$$ from point (0, 0) and $$\left( {0,{1 \over {\sqrt 3 }}} \right)$$ is equal. Only if z is on a straight line then it will be equal distance from the both the points.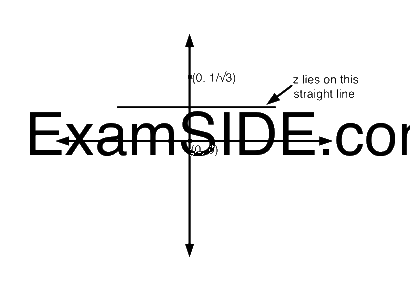
$$\therefore$$ $${{\left| z \right|} \over {\left| {z - {1 \over {\sqrt 3 }}i} \right|}} = \left| \omega \right|$$
$$ \Rightarrow $$ $${{\left| z \right|} \over {\left| {z - {1 \over {\sqrt 3 }}i} \right|}} = 1$$
$$ \Rightarrow $$ $$\left| z \right| = \left| {z - {1 \over {\sqrt 3 }}i} \right|$$ ..........equation (1)
$$\left| z \right|$$ represent distance of $$z$$ from point (0, 0) and
$$\left| {z - {1 \over {\sqrt 3 }}i} \right|$$ represent distance of $$z$$ from point $$\left( {0,{1 \over {\sqrt 3 }}} \right)$$.
According to the equation (1) the distance of $$z$$ from point (0, 0) and $$\left( {0,{1 \over {\sqrt 3 }}} \right)$$ is equal. Only if z is on a straight line then it will be equal distance from the both the points.

Comments (0)


