JEE MAIN - Mathematics (2005 - No. 34)
If a vertex of a triangle is $$(1, 1)$$ and the mid points of two sides through this vertex are $$(-1, 2)$$ and $$(3, 2)$$ then the centroid of the triangle is :
$$\left( { - 1,{7 \over 3}} \right)$$
$$\left( {{{ - 1} \over 3},{7 \over 3}} \right)$$
$$\left( { 1,{7 \over 3}} \right)$$
$$\left( {{{ 1} \over 3},{7 \over 3}} \right)$$
Explanation
Vertex of triangle is $$\left( {1,\,1} \right)$$ and midpoint of sides through -
this vertex is $$\left( { - 1,\,2} \right)$$ and $$\left( {3,2} \right)$$
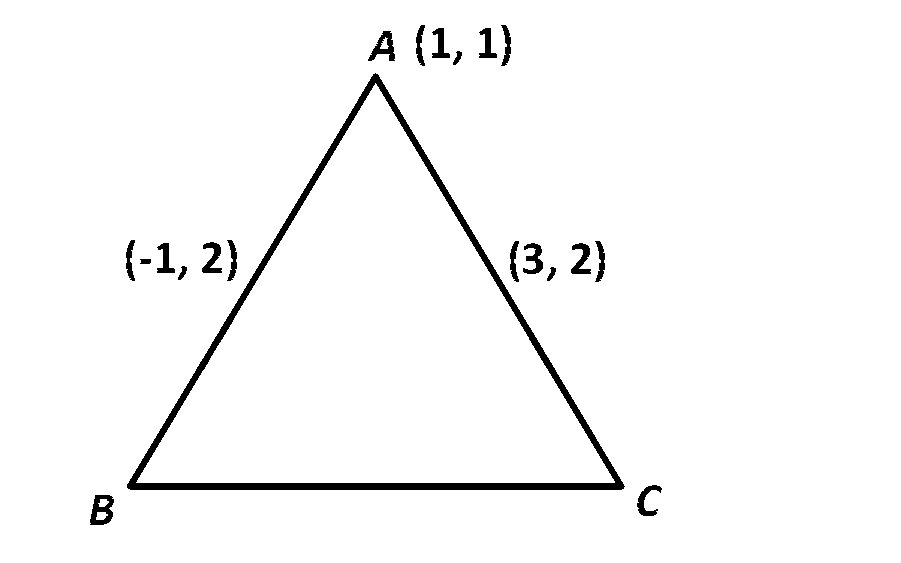
$$ \Rightarrow $$ vertex $$B$$ and $$C$$ come out to be $$\left( { - 3,3} \right)$$ and $$\left( {5,3} \right)$$
$$\therefore$$ centroid is $${{1 - 3 + 5} \over 3},{{1 + 3 + 5} \over 3} \Rightarrow \left( {1,{7 \over 3}} \right)$$
this vertex is $$\left( { - 1,\,2} \right)$$ and $$\left( {3,2} \right)$$

$$ \Rightarrow $$ vertex $$B$$ and $$C$$ come out to be $$\left( { - 3,3} \right)$$ and $$\left( {5,3} \right)$$
$$\therefore$$ centroid is $${{1 - 3 + 5} \over 3},{{1 + 3 + 5} \over 3} \Rightarrow \left( {1,{7 \over 3}} \right)$$
Comments (0)


