JEE MAIN - Mathematics (2005 - No. 22)
The parabolas $${y^2} = 4x$$ and $${x^2} = 4y$$ divide the square region bounded by the lines $$x=4,$$ $$y=4$$ and the coordinate axes. If $${S_1},{S_2},{S_3}$$ are respectively the areas of these parts numbered from top to bottom ; then $${S_1},{S_2},{S_3}$$ is :
$$1:2:1$$
$$1:2:3$$
$$2:1:2$$
$$1:1:1$$
Explanation
Intersection points of $${x^2} = 4y$$ and $${y^2} = 4x$$ are $$\left( {0,0} \right)$$ and $$\left( {4,4} \right).$$ The graph is as shown in the figure.
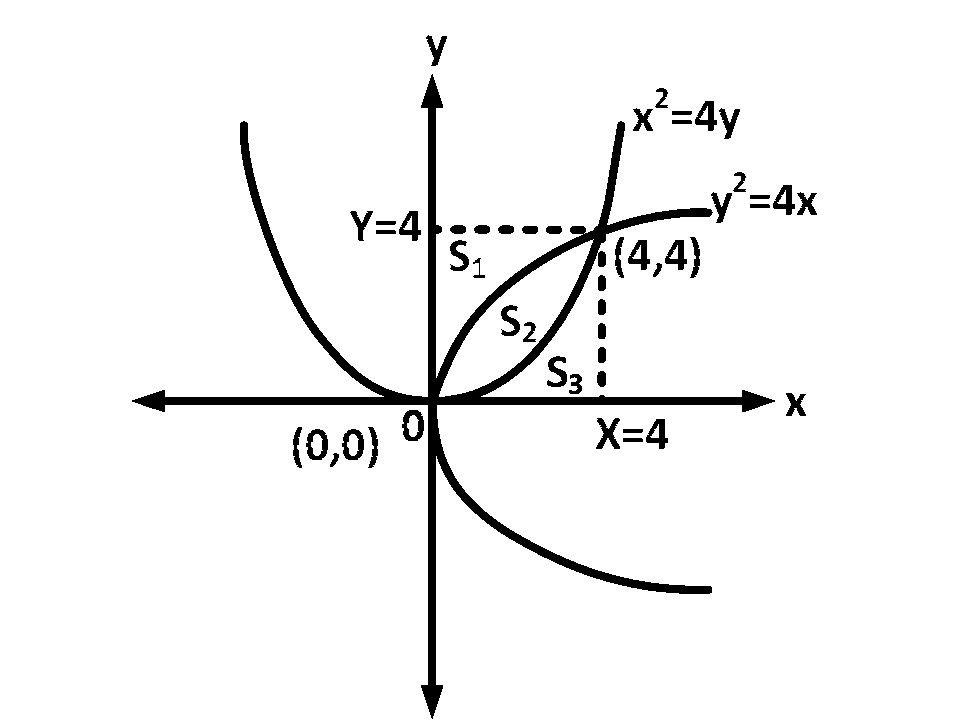
By symmetry, we observe
$${S_1} = {S_3} = \int\limits_0^4 {ydx = \int\limits_0^4 {{{{x^2}} \over 4}dx} } $$
$$ = \left[ {{{{x^3}} \over {12}}} \right]_0^4 = {{16} \over 3}$$ sq. unit
Also $${S_2} = \int\limits_0^4 {\left( {2\sqrt x - {{{x^2}} \over 4}} \right)} dx$$
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = \left[ {{{2{x^{{3 \over 2}}}} \over {{3 \over 2}}} - {{{x^3}} \over {12}}} \right]_0^4$$
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {4 \over 3} \times 8 - {{16} \over 3} = {{16} \over 3}$$
$$\therefore$$ $${S_1}:{S_2}:{S_3} = 1:1:1$$

By symmetry, we observe
$${S_1} = {S_3} = \int\limits_0^4 {ydx = \int\limits_0^4 {{{{x^2}} \over 4}dx} } $$
$$ = \left[ {{{{x^3}} \over {12}}} \right]_0^4 = {{16} \over 3}$$ sq. unit
Also $${S_2} = \int\limits_0^4 {\left( {2\sqrt x - {{{x^2}} \over 4}} \right)} dx$$
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = \left[ {{{2{x^{{3 \over 2}}}} \over {{3 \over 2}}} - {{{x^3}} \over {12}}} \right]_0^4$$
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {4 \over 3} \times 8 - {{16} \over 3} = {{16} \over 3}$$
$$\therefore$$ $${S_1}:{S_2}:{S_3} = 1:1:1$$
Comments (0)


