JEE MAIN - Mathematics (2005 - No. 13)
Area of the greatest rectangle that can be inscribed in the
ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$
ellipse $${{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1$$
$$2ab$$
$$ab$$
$$\sqrt {ab} $$
$${a \over b}$$
Explanation
Area of rectangle $$ABCD$$ $$ = 2a\,\cos \,\theta $$
$$\left( {2b\,\sin \,\theta } \right) = 2ab\,\sin \,2\theta $$
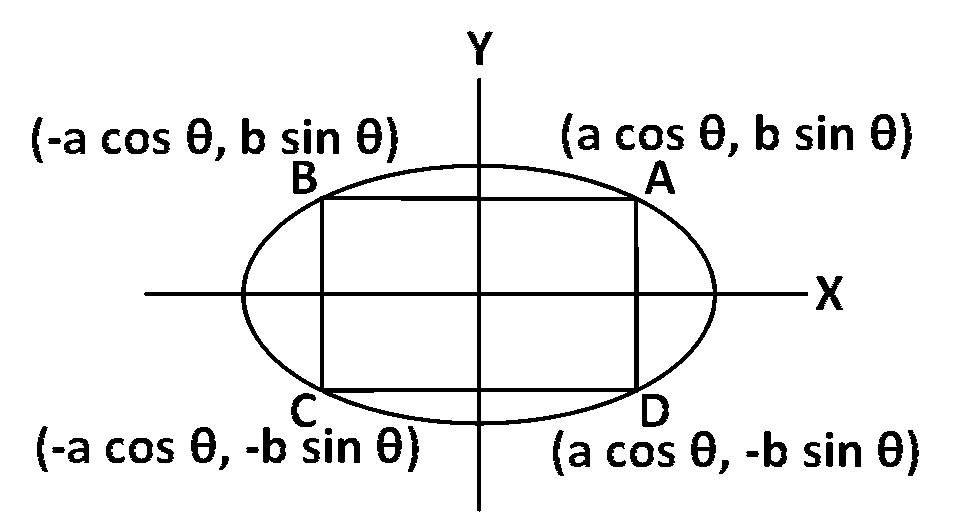
$$ \Rightarrow $$ Area of greatest rectangle is equal to $$2ab$$
When $$\sin \,2\theta = 1.$$
$$\left( {2b\,\sin \,\theta } \right) = 2ab\,\sin \,2\theta $$

$$ \Rightarrow $$ Area of greatest rectangle is equal to $$2ab$$
When $$\sin \,2\theta = 1.$$
Comments (0)


