JEE MAIN - Mathematics (2004 - No. 4)
The graph of the function y = f(x) is symmetrical about the line x = 2, then
$$f\left( x \right) = - f\left( { - x} \right)$$
$$f\left( {2 + x} \right) = f\left( {2 - x} \right)$$
$$f\left( x \right) = f\left( { - x} \right)$$
$$f\left( {x + 2} \right) = f\left( {x - 2} \right)$$
Explanation
Let us consider a graph symm. with respect to line $$x=2$$ as shown in the figure.
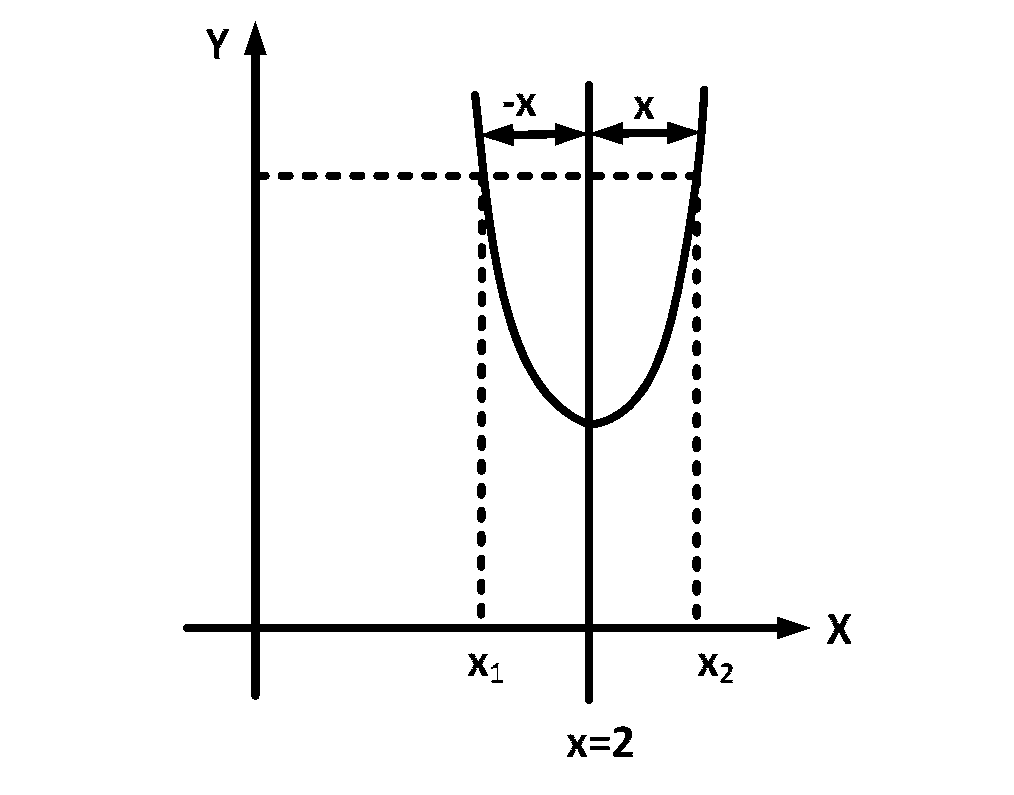
From the figure
$$f\left( {{x_1}} \right) = f\left( {{x_2}} \right),$$
where $${x_1} = 2 - x$$ and $${x_2} = 2 + x$$
$$\therefore$$ $$\,\,\,\,f\left( {2 - x} \right) = f\left( {2 + x} \right)$$

From the figure
$$f\left( {{x_1}} \right) = f\left( {{x_2}} \right),$$
where $${x_1} = 2 - x$$ and $${x_2} = 2 + x$$
$$\therefore$$ $$\,\,\,\,f\left( {2 - x} \right) = f\left( {2 + x} \right)$$
Comments (0)


