JEE MAIN - Mathematics (2004 - No. 22)
The area of the region bounded by the curves
$$y = \left| {x - 2} \right|,x = 1,x = 3$$ and the $$x$$-axis is :
$$y = \left| {x - 2} \right|,x = 1,x = 3$$ and the $$x$$-axis is :
$$4$$
$$2$$
$$3$$
$$1$$
Explanation
The required area is shown by shaded region
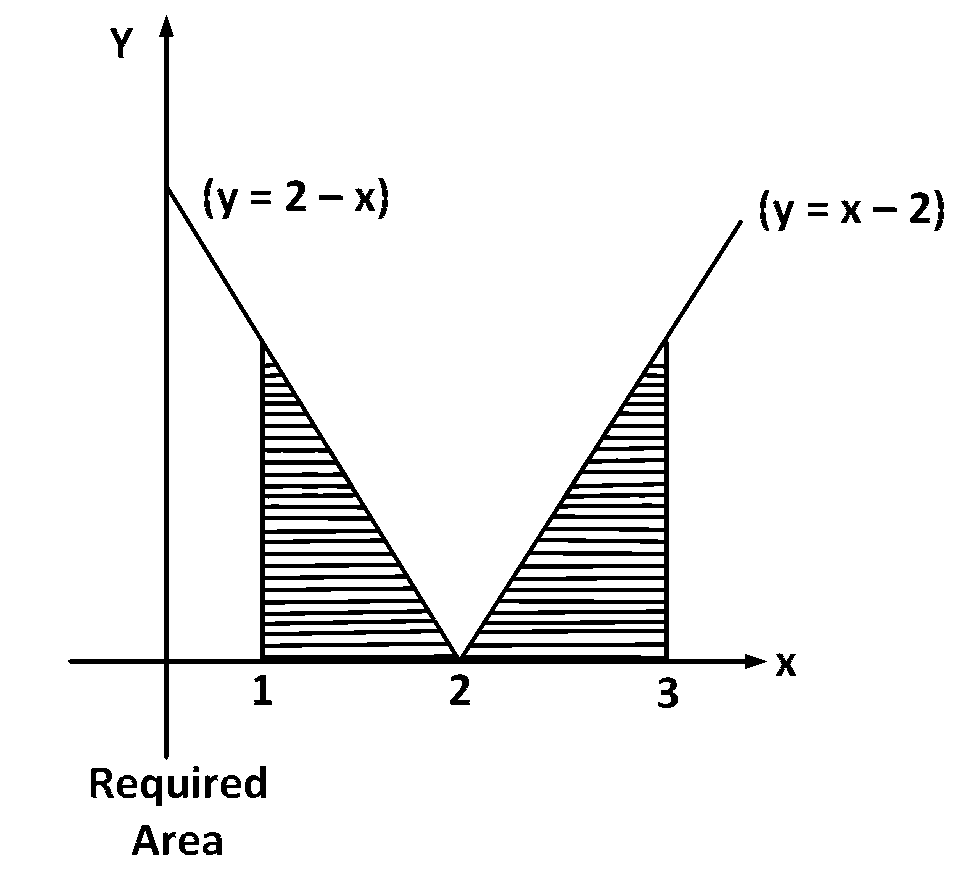
$$A = \int\limits_1^3 {\left| {x - 2} \right|dx = 2\int\limits_2^3 {\left( {x - 2} \right)} } dx$$
$$ = 2\left[ {{{{x^2}} \over 2} - 2x} \right]_2^3 = 1$$

$$A = \int\limits_1^3 {\left| {x - 2} \right|dx = 2\int\limits_2^3 {\left( {x - 2} \right)} } dx$$
$$ = 2\left[ {{{{x^2}} \over 2} - 2x} \right]_2^3 = 1$$
Comments (0)


