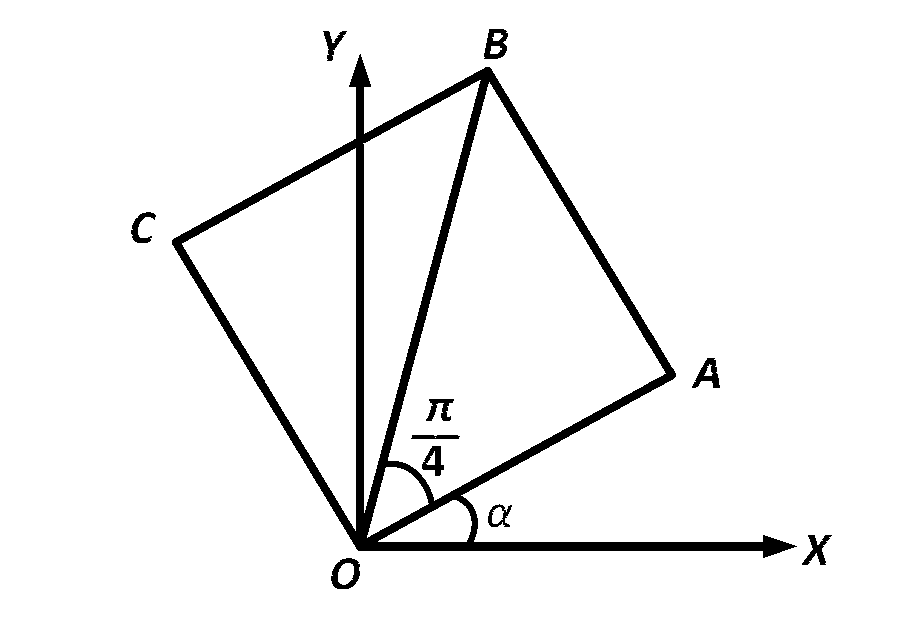
Co-ordinate of $$A = \left( {a\,\cos \,\alpha ,\,\,a\,\sin \,\alpha } \right)$$

Equation of $$OB,$$

$$y = \tan \left( {{\pi \over 4} + \alpha } \right)x$$

$$CA{ \bot ^r}$$ to $$OB$$

$$\therefore$$ slope of $$CA=-$$ $$\cot \left( {{\pi \over 4} + \alpha } \right)$$

Equation of $$CA$$

$$y - a\sin \alpha = - cot\left( {{\pi \over 4} + \alpha } \right)\left( {x - a\,\cos \,\alpha } \right)$$

$$ \Rightarrow \left( {y - a\sin \alpha } \right)\left( {\tan \left( {{\pi \over 4} + \alpha } \right)} \right) = \left( {a\,\cos \,\alpha - x} \right)$$

$$ \Rightarrow \left( {y - a\sin \alpha } \right)\left( {{{\tan {\pi \over 4} + \tan \alpha } \over {1 - \tan {\pi \over 4}\tan \alpha }}} \right)\left( {a\,\cos \,\alpha - x} \right)$$

$$ \Rightarrow \left( {y - a\sin \alpha } \right)\left( {1 + \tan \alpha } \right) = \left( {a\cos \alpha - x} \right)\left( {1 - \tan \alpha } \right)$$

$$ \Rightarrow \left( {y - a\sin \alpha } \right)\left( {\cos \alpha + \sin \alpha } \right) = \left( {a\cos \alpha - x} \right)\left( {\cos \alpha - \sin \alpha } \right)$$

$$ \Rightarrow y\left( {\cos + \sin \alpha } \right) - a\sin \alpha \cos \alpha - a{\sin ^2}\alpha $$

$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a{\cos ^2}\alpha - a\cos \alpha \sin \alpha - x\left( {\cos \alpha - \sin \alpha } \right)$$

$$ \Rightarrow y\left( {\cos \alpha + sin\alpha } \right) + x\left( {\cos \alpha - \sin \alpha } \right) = a$$

$$y\left( {\sin \alpha + \cos \alpha } \right) + x\left( {\cos \alpha - \sin \alpha } \right) = a.$$