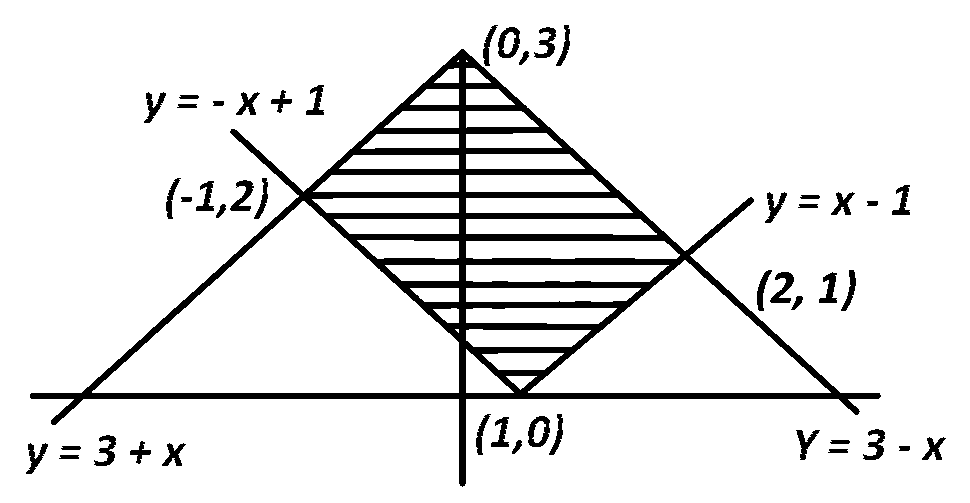
$$A = \int\limits_{ - 1}^0 {\left\{ {\left( {3 + x} \right) - \left( { - x + 1} \right)} \right\}dx + } $$

$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$\int\limits_0^1 {\left\{ {\left( {3 - x} \right) - \left( { - x + 1} \right)} \right\}dx + } $$

$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$\int\limits_1^2 {\left\{ {\left( {3 - x} \right) - \left( {x - 1} \right)} \right\}dx} $$

$$ = \int\limits_{ - 1}^0 {\left( {2 + 2x} \right)dx + \int\limits_0^1 {2dx + \int\limits_1^2 {\left( {4 - 2x} \right)dx} } } $$

$$ = \left[ {2x - {x^2}} \right]_{ - 1}^0 + \left[ {2x} \right]_0^1 + \left[ {4x - {x^2}} \right]_1^2$$

$$ = 0 - \left( { - 2 + 1} \right) + \left( {2 - 0} \right) + \left( {8 - 4} \right) - \left( {4 - 1} \right)$$

$$ = 1 + 2 + 4 - 3 = 4$$ sq. units