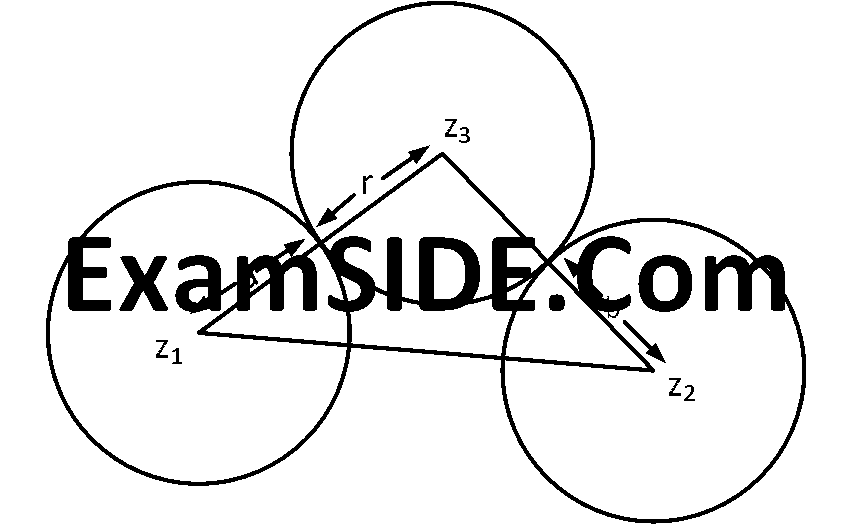Let the circle be $$\left| {z - {z_3}} \right| = r.$$

Then according to given conditions

$$\left| {{z_3} - {z_1}} \right| = r + a$$ (Shown in the image)

and $$\left| {{z_3} - {z_2}} \right| = r + b.$$ (Shown in the image)

Eliminating $$r,$$ we get

$$\left| {{z_3} - {z_1}} \right| - \left| {{z_3} - {z_2}} \right| = a - b.$$

$$\therefore$$ Locus of center $${z_3}$$ is

$$\left| {z - {z_1}} \right| - \left| {z - {z_2}} \right| = a - b$$ = constant.

Definition of hyperbola says, when difference of distance between two points is constant from a particular point then that particular point will lie on a hyperbola.

Here distance of z₁ from z₃ is = $$r + a$$ and distance of z₂ from z₃ is = $$r + b$$

Now their difference = ($$r + a$$) - ($$r + b$$) = $$a - b$$ = a constant

$$\therefore$$ Locus of z₃ is a hyperbola.