JEE MAIN - Chemistry (2009 - No. 22)
Using MO theory, predict which of the following species has the shortest bond length?
$$O_2^+$$
$$O_2^-$$
$$O_2^{2-}$$
$$O_2^{2+}$$
Explanation
Note :
(1) $$\,\,\,\,$$ Bond length $$ \propto $$ $${1 \over {Bond\,\,order}}$$
(2) $$\,$$ Bond order $$ = {1 \over 2}$$ [Nb $$-$$ Na]
Nb = No of electrons in bonding molecular orbital
Na $$=$$ No of electrons in anti bonding molecular orbital
(4) $$\,\,\,\,$$ upto 14 electrons, molecular orbital configuration is
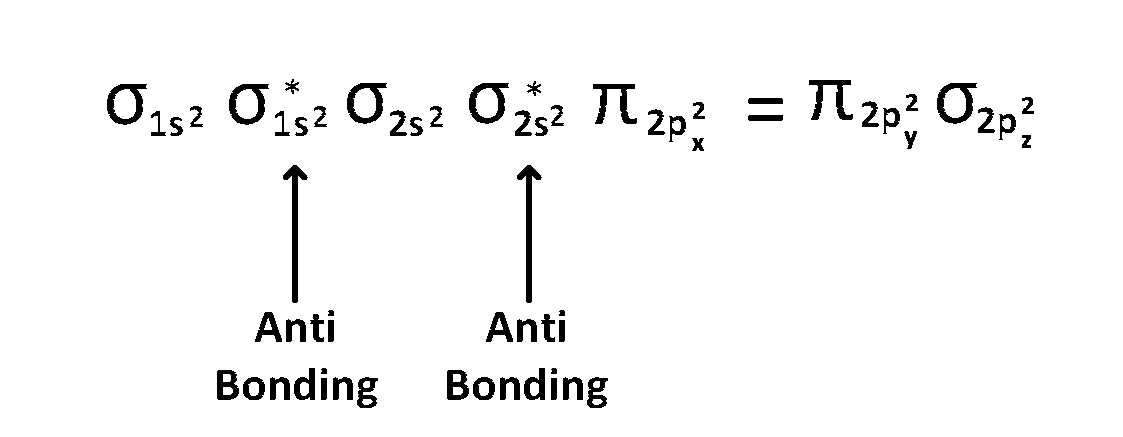
Here Na = Anti bonding electron $$=$$ 4 and Nb = 10
(5) $$\,\,\,\,$$ After 14 electrons to 20 electrons molecular orbital configuration is - - -
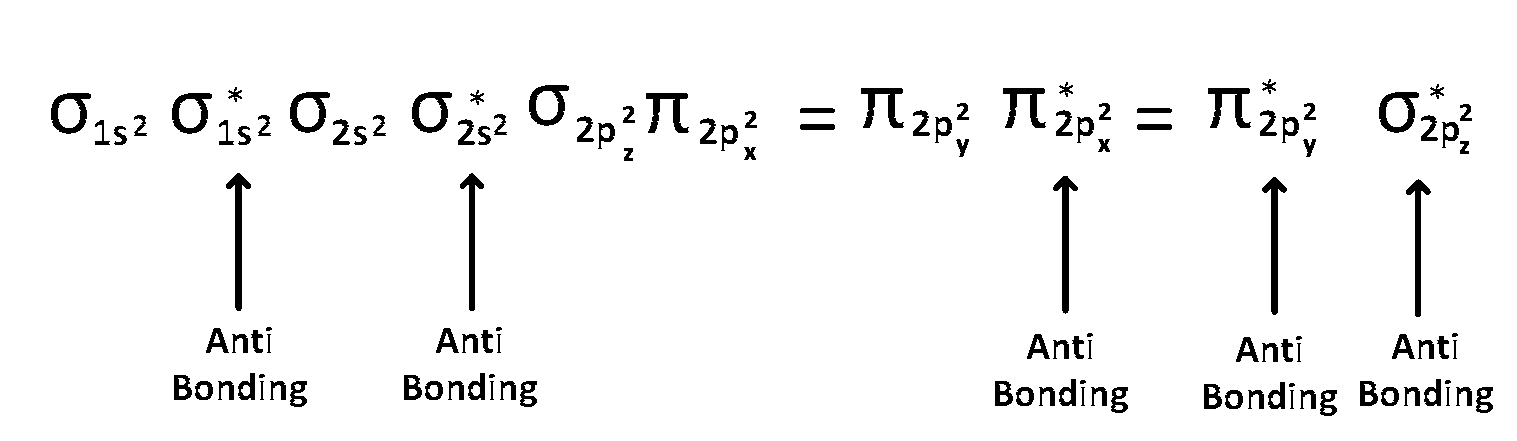
Here Na = 10
and Nb = 10
In O atom 8 electrons present, so in O2, 8 $$ \times $$ 2 = 16 electrons present.
Then in $$O_2^ + $$ no of electrons = 15
in $$O_2^ - $$ no of electrons = 17
in $$O_2^{2 - }$$ no of electrons = 18
$$\therefore\,\,\,\,$$ Molecular orbital configuration of O2 (16 electrons) is
$${\sigma _{1{s^2}}}\,\,\sigma _{1{s^2}}^ * \,$$ $${\sigma _{2{s^2}}}\,\,\sigma _{2{s^2}}^ * \,$$ $${\sigma _{2p_z^2}}\,\,{\pi _{2p_x^2}} = {\pi _{2p_y^2}}\,\,\pi _{2p_x^1}^ * \,\, = \pi _{2p_y^1}^ * $$
$$\therefore\,\,\,\,$$Na = 6
Nb = 10
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 6} \right] = 2$$
Molecular orbital configuration of O$$_2^ + $$ (15 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^1}^ * \, = \,\pi _{2p_y^o}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 5
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 5} \right]$$ = 2.5
Molecular orbital configuration of O$$_2^ {2+ }$$ (14 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^0}^ * \, = \,\pi _{2p_y^o}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 4
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 4} \right]$$ = 3
Molecular orbital configuration of $$O_2^ - $$ (17 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^2}^ * \, = \,\pi _{2p_y^1}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 7
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 7} \right]$$ = 1.5
Molecular orbital configuration of O $$_2^{2 - }$$ (18 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^2}^ * \, = \,\pi _{2p_y^2}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 8
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}$$ [ 10 $$-$$ 8] = 1
As Bond length $$ \propto $$ $${1 \over {Bond\,\,order}}$$
So $$O_2^{2+}$$ has the shortest bond length.
(1) $$\,\,\,\,$$ Bond length $$ \propto $$ $${1 \over {Bond\,\,order}}$$
(2) $$\,$$ Bond order $$ = {1 \over 2}$$ [Nb $$-$$ Na]
Nb = No of electrons in bonding molecular orbital
Na $$=$$ No of electrons in anti bonding molecular orbital
(4) $$\,\,\,\,$$ upto 14 electrons, molecular orbital configuration is

Here Na = Anti bonding electron $$=$$ 4 and Nb = 10
(5) $$\,\,\,\,$$ After 14 electrons to 20 electrons molecular orbital configuration is - - -
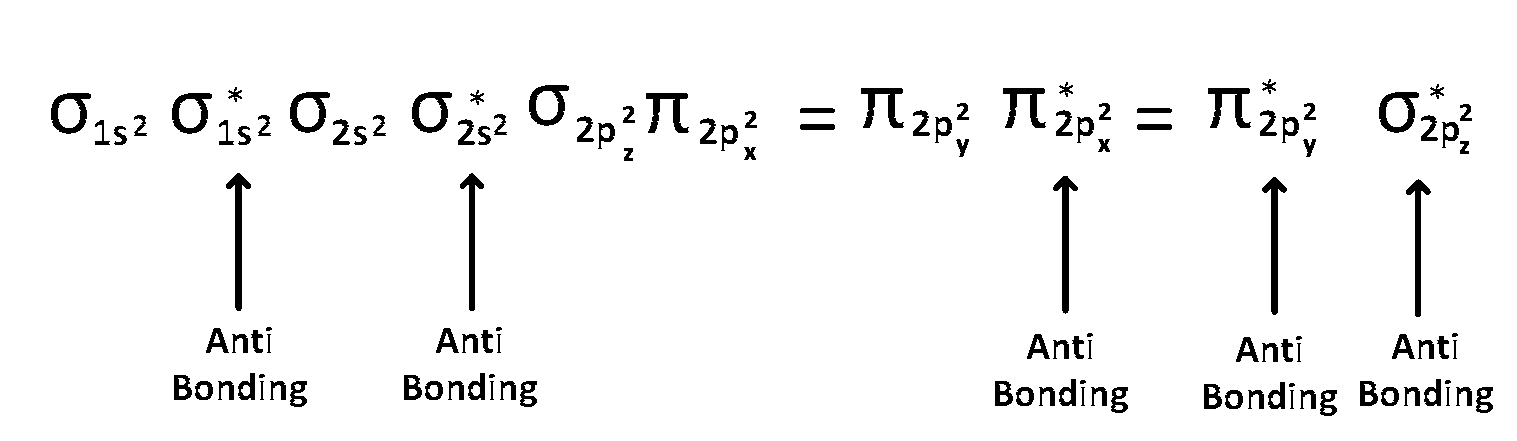
Here Na = 10
and Nb = 10
In O atom 8 electrons present, so in O2, 8 $$ \times $$ 2 = 16 electrons present.
Then in $$O_2^ + $$ no of electrons = 15
in $$O_2^ - $$ no of electrons = 17
in $$O_2^{2 - }$$ no of electrons = 18
$$\therefore\,\,\,\,$$ Molecular orbital configuration of O2 (16 electrons) is
$${\sigma _{1{s^2}}}\,\,\sigma _{1{s^2}}^ * \,$$ $${\sigma _{2{s^2}}}\,\,\sigma _{2{s^2}}^ * \,$$ $${\sigma _{2p_z^2}}\,\,{\pi _{2p_x^2}} = {\pi _{2p_y^2}}\,\,\pi _{2p_x^1}^ * \,\, = \pi _{2p_y^1}^ * $$
$$\therefore\,\,\,\,$$Na = 6
Nb = 10
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 6} \right] = 2$$
Molecular orbital configuration of O$$_2^ + $$ (15 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^1}^ * \, = \,\pi _{2p_y^o}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 5
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 5} \right]$$ = 2.5
Molecular orbital configuration of O$$_2^ {2+ }$$ (14 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^0}^ * \, = \,\pi _{2p_y^o}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 4
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 4} \right]$$ = 3
Molecular orbital configuration of $$O_2^ - $$ (17 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^2}^ * \, = \,\pi _{2p_y^1}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 7
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}\left[ {10 - 7} \right]$$ = 1.5
Molecular orbital configuration of O $$_2^{2 - }$$ (18 electrons) is
$${\sigma _{1{s^2}}}\,\sigma _{1{s^2}}^ * \,{\sigma _{2{s^2}}}\,\sigma _{2{s^2}}^ * \,{\sigma _{2p_z^2}}\,{\pi _{2p_x^2}}\, = \,{\pi _{2p_y^2}}\,\pi _{2p_x^2}^ * \, = \,\pi _{2p_y^2}^ * $$
$$\therefore\,\,\,\,$$ Nb = 10
Na = 8
$$\therefore\,\,\,\,$$ BO = $${1 \over 2}$$ [ 10 $$-$$ 8] = 1
As Bond length $$ \propto $$ $${1 \over {Bond\,\,order}}$$
So $$O_2^{2+}$$ has the shortest bond length.
Comments (0)


