JAMB - Physics (2023 - No. 23)
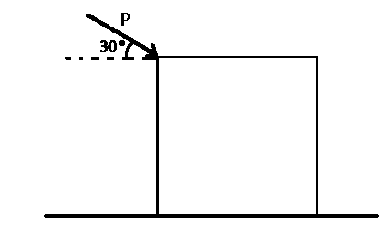
A 400 N box is being pushed across a level floor at a constant speed by a force P of 100 N at an angle of 30.0° to the horizontal, as shown in the the diagram below. What is the coefficient of kinetic friction between the box and the floor?
Explanation
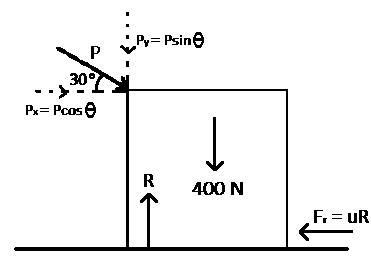
W = 400 N; P = 100 N; θ = 30o; μ = ?
Frictional force (Fr) = μR (where R is the normal reaction)
The forces acting along the horizontal direction are Fr and Px
∴ Pcos 30° - Fr = ma (Pcos 30° is acting in the +ve x-axis while Fr in the -ve x-axis)
⇒ 100cos 30° - μR = ma
Since the box is moving at constant speed, its acceleration is zero
⇒ 100cos 30° - μR = 0
⇒ 100cos 30o = μR ----- (i)
The forces acting in the vertical direction are W, Py and R
∴ R - Psin 30° - W = 0 (R is acting upward (+ve) while Py and W are acting downward (-ve) and they are at equilibrium)
⇒ R - 100sin 30° - 400 = 0
⇒ R = 100sin 30° + 400
⇒ R = 50 + 400 = 450 N
From equation (i)
⇒ 100cos 30° = 450μ
⇒μ=100cos30°
N = \(\frac{100cos30°}{450}\)
= μ = 0.19
Comments (0)


