JAMB - Physics (2020 - No. 23)
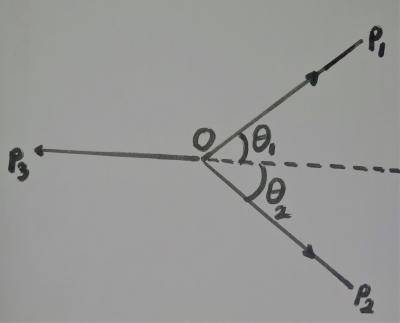
Consider the three forces acting at O and in equilibrium as shown in the figure. Which of the following equations is/are CORRECT?
I. P\(_1\) cos \(\theta_1\) = p\(_1\) cos \(\theta_2\)
II. P\(_3\) = P\(_1\) cos \(\theta_4\) + P\(_2 cos_2\)
III. P\(_1 \sin \theta_1 = P_2 \sin \theta_2\)
Explanation
resolving \(P_1\), \(P_2\) and \(P_3\) into x and y component
\(P_x\) = \(P_1 Cos\theta_1\)
\(P_y\) = \(P_1Sin\theta_1\)
\(P_x\) = \(P_2Cos\theta_2\)
\(P_y\) = \(-P_2Sin \theta_2\)
\(P_x\) = \(- P_3Cos \theta0\)
therefore
total \(P_x\) = \(P_1 Cos\theta_1\) + \(P_2Cos \theta_2\) + \(- P_3Cos \theta0\) = 0
total \(P_y\) = \(P_1Sin\theta_1\) + \(-P_2Sin \theta_2\) = 0
so that \(P_1Sin\theta_1\) = \(P_2Sin \theta_2\)
\( P_3Cos \theta0\) = \(P_1 Cos\theta_1\) + \(P_2Cos \theta_2\)
Comments (0)


