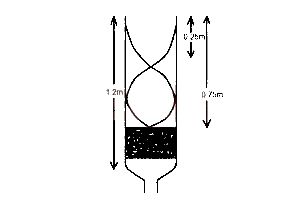
In vibration in a closed pipe/tube, the first resonance occurs at a position L = V/4f,
When reading from the top of the tube,

 L\(_1\) = \(\frac{340}{4 \times 340}\) = 0.25m

= 0.25m
L\(_2\) = \(\frac{3V}{4f}\)

L\(_2\) = \(\frac{3 \times 340}{4 \times 340}\)

= 0.75m
L\(_3\) = \(\frac{5V}{4f}\)

L\(_3\) = \(\frac{5\times 340}{4\times 340}\)

= 1.25m

However, the effective length of the tube is 1.2m. Thus reading from below, the first position of resonance will be 1.20 - 0.25m = 0.95m