JAMB - Mathematics (2024 - No. 21)

Find the perimeter of a triangle whose vertices pass through ( 3, 2), (4, 5) and (6, 2) in surd form.

3 + \(\sqrt{12} + \sqrt{13}\)

3 - \(\sqrt{10} + \sqrt{13}\)

3 + \(\sqrt{10} + \sqrt{13}\)

3 - \(\sqrt{12} + \sqrt{13}\)

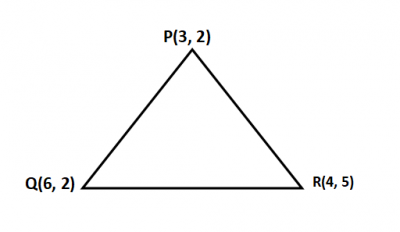
From the diagram above, Calculate the distance between any two vertices as follows.

PQ = \(\sqrt{(6 - 3)^2 + (2-2)^2}\) = \(\sqrt{9}\) = 3

QR = \(\sqrt{(6 - 4)^2 + (2-5)^2}\) = \(\sqrt{13}\)

PR = \(\sqrt{(4 - 3)^2 + (5 - 1)^2}\) = \(\sqrt{10}\)

\(\therefore\), perimeter = 3 + \(\sqrt{13}\) + \(\sqrt{10}\)