JAMB - Mathematics (2023 - No. 10)
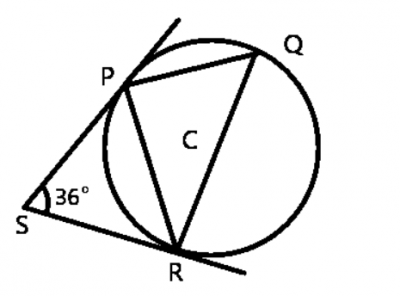
The diagram above is a circle with centre C. P, Q and S are points on the circumference. PS and SR are tangents to the circle. ∠PSR = 36\(^o\). Find ∠PQR
72\(^0\)
36\(^0\)
144\(^0\)
54\(^0\)
Explanation
From ∆PSR
|PS| = |SR| (If two tangents are drawn from an external point of the circle, then they are of equal lengths)
∴ ∆PSR is isosceles
∠PSR + ∠SRP + ∠SPR = 180\(^o\) (sum of angles in a triangle)
Since |PS| = |SR|; ∠SRP = ∠SPR
⇒ ∠PSR + ∠SRP + ∠SRP = 180\(^o\)
∠PSR + 2∠SRP = 180\(^o\)
36\(^o\) + 2∠SRP = 180\(^o\)
2∠SRP = 180\(^o\) - 36\(^o\)
2∠SRP = 144\(^o\)
∠SRP = \(\frac {144^o}{2} = 72^0\)
∠SRP = ∠PQR (angle formed by a tangent and chord is equal to the angle in the alternate segment)
∴ ∠PQR = 72\(^0\)
Comments (0)


