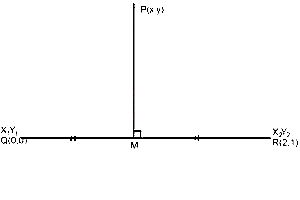
Locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1) is the perpendicular bisector of the straight line joining Q and R
Mid point QR = \(\frac{x_2 + x_1}{2}, \frac{y_2 + y_1}{2}\)
= \(\frac{2 + 0}{2}, \frac{1 + 0}{2}\)

= \((1, \frac{1}{2})\)

 Gradient of QR = \(\frac{y_{2} - y_{1}}{x_{2} - x_{1}}\)

= \(\frac{1 - 0}{2 - 0}\)

= \(\frac{1}{2}\)

Gradient of PM = \(\frac{-1}{\frac{1}{2}}\)
= -2
Equation of PM = y - y\(_1\) = m(x-x_\(_1\))
i.e y - 1/2 = -2(x-1)
2y - 1 = -4(x-1)
2y - 1 = -4x + 4
2y + 4x = 5