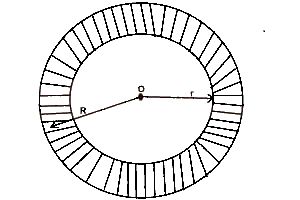
JAMB - Mathematics (2002 - No. 44)
21/25πR2
9/25πR2
21/23πR2
5/9πR2
Explanation
r = \(\frac{2}{3}\)R
∴R = \(\frac{3}{3}\)R
Area of small circle = πr2
= π(\(\frac{2R}{3}\))2
Area of the big circle πr2 = π\(\frac{(3R)^2}{3}\)
Area of shaded portion = π(\(\frac{3R}{3}\))2 - π(\(\frac{2R}{3}\))2
= π[(\(\frac{3R}{3}\))2 - (\(\frac{2R}{3}\))2]
= π[(\(\frac{3R}{3}) + (\frac{2R}{3}) - (\frac{3R}{3}\)) - (\(\frac{2R}{3}\))]
= π[(\(\frac{5R}{3}\)) (\(\frac{R}{3}\))]
= π x \(\frac{5R}{3}\) x \(\frac{R}{3}\)
= 5/9πR2
∴R = \(\frac{3}{3}\)R
Area of small circle = πr2
= π(\(\frac{2R}{3}\))2
Area of the big circle πr2 = π\(\frac{(3R)^2}{3}\)
Area of shaded portion = π(\(\frac{3R}{3}\))2 - π(\(\frac{2R}{3}\))2
= π[(\(\frac{3R}{3}\))2 - (\(\frac{2R}{3}\))2]
= π[(\(\frac{3R}{3}) + (\frac{2R}{3}) - (\frac{3R}{3}\)) - (\(\frac{2R}{3}\))]
= π[(\(\frac{5R}{3}\)) (\(\frac{R}{3}\))]
= π x \(\frac{5R}{3}\) x \(\frac{R}{3}\)
= 5/9πR2
Comments (0)


