JAMB - Mathematics (2002 - No. 41)
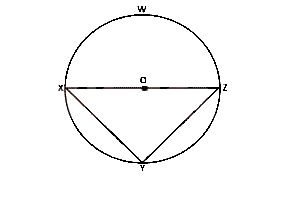
In the diagram above , XZ is the diameter of the circle XZW, with center O and radius 15/2 cm. If XY = 12 cm, find the area of the triangle XYZ
54 cm2
45 cm2
27 cm2
75 cm2
Explanation
Since radius = \(\frac{15}{2}\) diameter = 2 * (\(\frac{15}{2}\)) = 15cm
XYZ is a right-angled triangle (since <Y = 90º )
∴ 15\(^2\) = 12\(^2\) + (YZ)\(^2\)
225 = 144 = (YZ)\(^2\)
225 - 144 = (YZ)\(^2\)
81 = (YZ)\(^2\)
\(\sqrt{81}\) = YZ
9 = YZ
Area of ΔXYZ = \(\frac{1}{2}\)bh
(\(\frac{1}{2}\) x 9 x 12
9 x 6 = 54
= 54cm\(^2\)
XYZ is a right-angled triangle (since <Y = 90º )
∴ 15\(^2\) = 12\(^2\) + (YZ)\(^2\)
225 = 144 = (YZ)\(^2\)
225 - 144 = (YZ)\(^2\)
81 = (YZ)\(^2\)
\(\sqrt{81}\) = YZ
9 = YZ
Area of ΔXYZ = \(\frac{1}{2}\)bh
(\(\frac{1}{2}\) x 9 x 12
9 x 6 = 54
= 54cm\(^2\)
Comments (0)


