JAMB - Mathematics (2001 - No. 38)
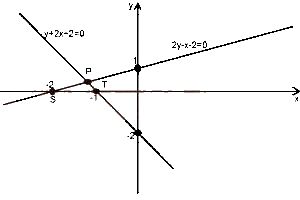
Triangle SPT is the solution of the linear inequalities
2y - x - 2 ≤ 0, y + 2x + 2 ≥ 0, -2 ≤ x ≤ - 1
-2 ≤ x ≤ 2, y ≥ 0, y + 2x + 2 ≤ 0, x ≤ 0
2y - x - 2 ≤ 0, y + 2x + 2 ≤ 0, y ≥ 0, x ≤ 0
2y - x - 2 ≥ 0, y + 2x + 2 ≤ 0, x ≤ 0
Explanation
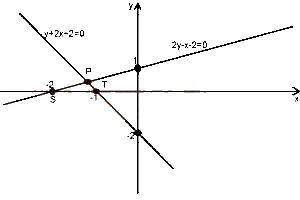
The two major lines have their lower portions involved. Since there are no broken lines here,\(\leq\) will hold for the two major lines
that is, 2y - x - 2 = 0 becomes 2y - x - 2 \(\leq\) 0
y + 2x + 2 = 0 becomes y + 2x + 2 \(\leq\) 0
Triangle SPT is located at the positive side of the y-axis, so y \(\geq\) 0, and the negative side of the x-axis so, x \(\leq\)
Therefore, OPTION C is correct.
Comments (0)


