JAMB - Mathematics (1989 - No. 36)
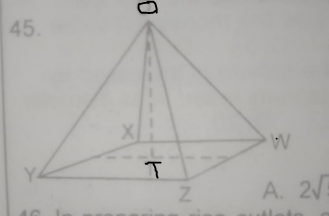
OXYZW is a pyramid with a square base such that OX = OY= OZ = OW = 5cm and XY = XW = YZ = WZ = 6cm. Find the height OT
2\(\sqrt{5}\)
3
4
4\(\sqrt{3}\)
Explanation
xz\(^2\) = 6\(^2\) + 6\(^2\)
36 + 36 = 72
xz = \(\sqrt{72}\)
6\(\sqrt{2}\) = XT
\(\frac{6\sqrt{2}}{2}\) = \(\frac{3}{\sqrt{2}}\)
OT\(^2\) = 5\(^2\) + (3\(\sqrt{2}\))2 = 25 + 18
OT = 4\(\sqrt{3}\)
36 + 36 = 72
xz = \(\sqrt{72}\)
6\(\sqrt{2}\) = XT
\(\frac{6\sqrt{2}}{2}\) = \(\frac{3}{\sqrt{2}}\)
OT\(^2\) = 5\(^2\) + (3\(\sqrt{2}\))2 = 25 + 18
OT = 4\(\sqrt{3}\)
Comments (0)


