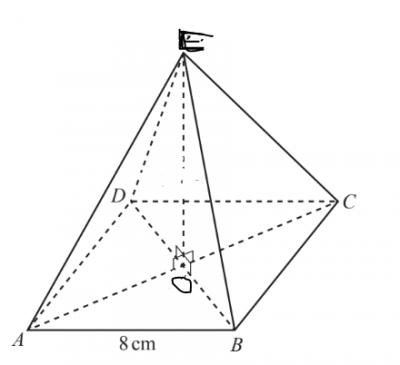
Base of pyramid of a square of side 8cm vertex directly above the centre edge = \(4\sqrt{3}\)cm

From the diagram, the diagonal of one base is AC\(^2\) = 8\(^2\) + 8\(^2\)

AC\(^2\) = 64 + 64 = 128

AC = \(8\sqrt{2}\)

but OC = \(\frac{1}{2}\)AC = \(\frac{1}{2}\) x 8\(\sqrt{2}\) = \(4\sqrt{2}\)cm

OE = h = height

h\(^2\) = EC\(^2\) - OC\(^2\)
h\(^2\) = (\(4\sqrt{3}\))\(^2\) -  (\(4\sqrt{2}\))\(^2\)
h\(^2\) = 16 x 3 - 16 x 2
48 - 32 = 16
h = \(\sqrt{16}\)
= 4cm