JAMB - Mathematics (1980 - No. 45)

In the figure, FGHJ is a circle of radius 3cm centre O. FOH, GOJ are perpendicular diameters. With G as centre of an arc of a circle is drawn to pass through F and H. Find the length of the perimeter of the lunar portion shaded.

3\(\pi\)\(\sqrt{2 - 1}\)cm

\(\frac{9}{2}\)\(\pi\)cm

3 \(\pi\)(1 + \(\frac{2}{2}\))

3(1 + \(\frac{2}{2}\))

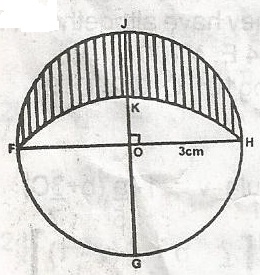
Explanation

Perimeter of lunar portion = 3\(\pi\) + \(\frac{3\pi \sqrt{2}}{2}\)

= 3 \(\pi\)(1 + \(\frac{2}{2}\))

JAMB - Mathematics (1980 - No. 45)

Explanation

Comments (0)