JAMB - Mathematics (1978 - No. 41)
The angle of elevation of the top of a vertical tower from a point A on the ground is 60o. From a point B, 2 units of distance further away from the foot of the tower, the angle of elevation of the tower is 45o. Find the distance of A from the foot of the tower
3 + \(\sqrt{3}\)
5 + \(\sqrt{3}\)
3 - \(\sqrt{3}\)
1
\(\sqrt{3}\) + 1
Explanation
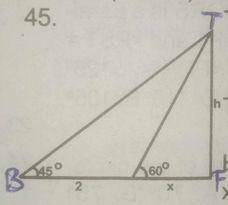
In < AFT: \(\frac{TF}{AF}\) = tan60º
therefore, TF = xtan60º ..................1
In < BFT: \(\frac{TF}{BF}\) = tan45º
TF = ( 2 + x )tan45º .......................2
equating equations 1 and 2
xtan60º = ( 2 + x )tan45º
But tan60º = \(\sqrt3\) and tan45º = 1
x \(\sqrt3\) = 2 + x
x \(\sqrt3\) - x = 2
x ( \(\sqrt3\) - 1) = 2
x = \(\frac{2}{(\sqrt3\)) - 1}\)
rationalizing the denominator x = \(\frac{2(\sqrt3 + 2)}{3 - 1}\) = \(\frac{2(\sqrt3 + 1)}{2}\) = \(\sqrt3\) + 1
Comments (0)


